DSC07088 (4)

106

Pochodna funkcji

Dokładna wartość ^55 = 3.9791....

c)    Przyjmujemy /(*) = arctg x, x₀ = 1. A* = 0.005. Wtedy

arctg 1.005 aarctg 1 + (arc tg*)^#|.«i'    ⁼ J ⁺ ITT “ ^0,7879

Dokładna wartość arc tg 1.005 = 0.7879....

d)    Przyjmujemy f{x) = 2\ xo = 3 ora* A* = -0.0001. Wtedy

2^xmw a 2^j + (2*)' |    • (-0.0001) = 8 - 8- In 2 -0.0001 = 7.9994... .

Dokładna wartość 2^J**^W# = 7.9994....

e)    Przyjmujemy /(x) = ch *, xo = 0 ora* A* = 0.07. Wtedy

chO.07a ch0+ (ch x)'|_ł-0-0.07 = l+ 0-0.07 = 1.000.

Dokładna wartość ch0.07 = 1.0025....

P) Przyjmujemy /(*) = (5 - 6x) ln(l + *), xo = 0 oraz Ax = 0.005. Wtedy mamy 4.97In 1.005 a 5ln 1 + [(5-flx)ln(l+x)j^-Ax

= 0+ f-61n(l+zR ⁽⁵~^6ig)1    -0.005 = 0.025.

L    I + X J iaO

Dokładna wartość 4.9Tb 1.005 ■ 0.024788....

• Przykład 4.14

a)    Do pomiaru wysokości wieży zamkowej zastosowano teodolit, którym można zmierzyć kąty z dokładnością 0.1°. Teodolit ustawiono w odległości d = 100 m od podstawy wieży i wycelowano na brzeg wierzchołka wieży (rysunek). Kąt jaki tworzy oś teodolitu z poziomem wynosi a = 35.7°. Z jaką w przybliżeniu dokładnością można obliczyć wysokość tej wieży?

b)    Krawędź sześcianu zmierzono z dokładnością 1 mm i otrzymano 125 mm. Z jaką w przybliżeniu dokładnością można obliczyć pole powierzchni całkowitej tego sześcianu?

Rozwiązanie

Jeżeli wielkości fizyczne x i y są związane zależnością y = /(x), to błąd bezwzględny Ay obliczanej wiełkcad y wyraża się wzorem przybliżonym

A,a*|/^/(xo)|A„

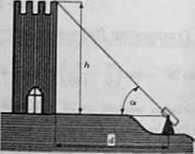
gdńe zc jest wynikiem pomiaru wielkości z, a A, jej błędem bezwzględnym, a) Wysokość wieży zamkowej jest określona wzorem h(a) = dtga. Dokładność Aa z jaką obliczamy wysokość wieży wyraża się w przybliżeniu wzorem Aa ~

|A'(oj| A₀. gdzie A® oznacza dokładność pcemAru kąta o (w radonach). Zatem

a 100 1    0.1°.x _

** ~ [ZSK\-uW~iav~°^02tBL

Dokładność pomiaru wysokości wieży wynosi około 0.20 m.

Przykłady

107

b) Pole powierzchni całkowitej sześcianu o krawędzi x wyraża się wzorem P(z) = Dokładność Af». z jaką obliczamy pole powierzchni całkowitej sześcianu wyraża się wzo^ rem przybliżonym

A, = 1^)1. A.,

gdzie A_s oznacza dokładność pomiaru krawędzi sześcianu. Zatem

Ap a* (12z|„_m • 1 = 1500mm³.

• Przykład 4.15

Korzystając z twierdzenia o pochodnej funkcji odwrotnej oraz z różniczki funkcji znaleźć przybliżone rozwiązania podanych równań: a)e^x+2x* 1.03; b) x⁷ + 4x® + 3** + 2x = 9.9962;

c) 2*-cos* = 3.14; d)    -0.999.

arc cos*

Rozwiązani#

a)    Rozważmy równanie

e" + 2x = p,

gdzie p jest parametrem. Ponieważ funkcja /(z) = e* + 2x jest rosnąca oraz ponieważ R jest jej zbiorem wartości, więc dla każdej wartości parametru p powyższe równanie ma jednoznaczne rozwiązanie

*=/-‘(p).

Ponadto mamy /"*( 1) = 0. Przyjmując teraz we wzorze przybliżonym /"* (po + Ap) sa /“* (po) + (Z^-1)' (po) Ap po •= 1 i Ap = 0.03 oraz korzystając ze wzoru na pochodną funkcji odwrotnej

(/*')'(po) = 7^. gdwpo = /(xo).

otrzymamy przybliżone rozwiązanie równania

e^m + 2x * 1.03.

Mamy zatem

^r‘W+7^ Ap-o₊^^.aos=aoi.

Uwaga. Dokładny pierwiastek tego równania jest równy 0.009083... .

b)    Rozważmy równanie

x^r + Ax^% + 3x^J + 2* = p,

gdzie p jest parametrem. Ponieważ funkcja /(*) ■ *^T+4x* +3x^J+2xj«t rosnąca oraz ponieważ R jest jej zbiorem wartości, więc dla każdej wartości parametru p powyższe równanie ma jednoznaczne rozwiązania

**r^łw-