DSC07087 (4)

104

Pochodne funkcji

b) | (Z"¹)'(3).    /(*) = +x+ 1;

•0 (y”¹)* (0. gd*«c $(*) =» 2C³* “ «"*•

Rozwiązanie

Jeżeli na otoczeniu punktu x₀ funkcja / jest dągła i ściśle monofoniczna oraz w tym punkcie ma pochodną wlaśdwą różną od 0. to pochodna funkcji odwrotnej wyo*/(zo) wyraża śę wzorem

a-i) FVmkcja odwrotna do funkcji y = /(*) = c“, gdzie z € R, ma postać z = f'^l(y) = by. gdzie y > 0. Do funkcji /^_ł stosujemy twierdzenie o pochodnej funkcji odwrotnej. Mamy    » jSffiif

arii) Funkcjo odwrotna do funkcji y = /(z) = ctgz, gdzie z € (O.tt), ma postać z = f -{y) = arcctgy, gdzie y G R. Z twierdzenia o pochodnej funkcji odwrotnej mamy

(arectgy)'

-I

-1

(ctgz)

l + ctg^az 1 + y^a ’

b-i) Zauważmy najpierw, że funkcja / jest ciągła i rosnąca na R. Ponadto /(1) = 3. Stąd wynika, że z = 1 jest jedynym rozwiązaniem równania

z*+z+ l=M

Funkcja / spełnia założenia twierdzenia o pochodnej funkcji odwrotnej, zatem mamy

(n'(3) = -sm =

m (2:+* + l)'U,    (5r* + l)|„_t    •'

b-i) Także w tym przykładzie funkcja g jest ciągła i rosnąca na R. Ponadto y(0) = L Stąd wynika, że z = 0 jest jedynym rozwiązaniem równania i unkcja y spełnia założenia twierdzenia o pochodnej funkcji odwrotnej, zatem mamy

• Prjyktad 4.12

Zakładając, źe funkcje / i g mają pochodne właściwe, obliczyć pochodne funkcji:

*) IN kg/wflto; ^b) y=

1 y I ®§1+9²(x); g) y

<«P/(x)

co8y(x)'

Przykłady

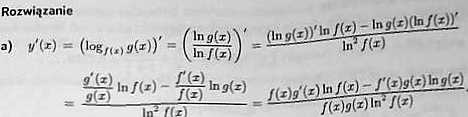
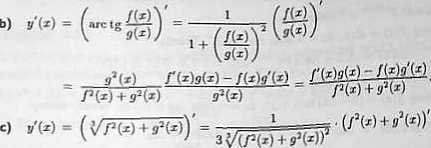
₌ 2 J(x)r(x) + g(x)g\x))

,,    ... _ fón/(x)Y _ (sin f(x))' cos g(x)-sln/frHco.gM)'

' *' \cosj(*) J    cefjH*)

. cos /(z) • cos g(x) • /'(z) -f sm f (x) -aag(x) • g'(z) cos² g{x)

Różniczka funkcji

• Przykład 4.13

Korzystając z różniczki funkcji obliczyć przybliżone wartości podanych wyrażeń: a) sin29°; b) ^63; c) arctg 1.005; d)    e) ch 0.07; f*) 4:97 ln 1.005.

Rozwiązanie

W obliczeniach przybliżonych stosujemy wzór:

/(xb + Aa:) «/(*ó) + / (xo) Az.

a) Przyjmujemy /(*) = sin z, xo = 30° = §|    = -1° = Wtedy

dn29° —"(j-jg) ««inf + (si_n*)'|    j (tŁ) = ff j^=⁰-⁴«9....

Dokładna wartość sin 29° = 0.4848.... b) Przyjmujemy /(z) = $5-1₀ = 64, Az = —1. Wtedy

^63 « ^64 h \_gmU ’ H) *= ⁴ “ gTjg *= 3.9792.....