DSCN1076 (2)

różnych liczb naturalnych dodatnich, to również liczba 2n jest

sumą kwadratów dwóch różnych liczb naturalnych dodatnich.

1.24. Wykazać, że jeśli iloczyn ab liczb naturalnych dodatnich a, b jest liczbą parzystą, to istnieją liczby naturalne dodatnie c, d takie, że a,² + b² + c² — d².

Jeśli iloczyn ab jest liczbą nieparzystą, to powyższe liczby nie istnieją.

1.25.    Wykazać, że jeśli dla liczb naturalnych m, n liczba

jest wymierna, to m, n są sześcianami liczb naturalnych.

1.26.    Wykazać, że dla każdej dodatniej liczby w takiej, że w² > 3 można dobrać liczbę neN+ tak, aby była spełniona nierówność:

3 ^<^^w““ jjJ^{2 <} w2‘

1.27. Wykazać, że dla każdej liczby naturalnej nieparzystej 3 iloczyn

jest podzielny przez liczbę n.

1.28. Wykazać, że jeśli spełnione są poniższe warunki:

1) aj + a₂ + ... + a* = 1,

2) b i + b₂ + ... + b_H = 1,

a?

*>i b₂

3)    a₁,a₂,...,a_neK₊o{0},

a%

+ /T + *

^b3

4) b_x.b₂.....b„eR₊, to

1.29. Wykazać, że dla każdej liczby naturalnej n > 2 spełnione są nierówności:

2 _____ __

■z y/9n — 1 < yjn — 1 + yjn + 1 < 2y/n.

gdy fc/n -1 gdy k|n.

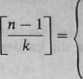
1.31. Znaleźć wszystkie liczby naturalne n spełniające równanie

%s|    |

Uwaga: Symbol [a] oznacza część całkowitą liczby a.

§ 2. Funkcje i ich własności

2.1    Znaleźć funkcję f: R-+ R taką, że dla każdego xeR spełnione są warunki:

/(2x) = 2/(x)-l i f(^x + 2) = 4 +/(x).

2.2    Znaleźć funkcję f:C->C taką, że dla każdej pary liczb całkowitych a, b spełnione są warunki:

f(a + b) =/(a) +/(b) + lab - 1 i /(-1) = 0.

Czy jest tylko jedna taka funkcja?

2.3. Znaleźć funkcjęf:R-+R nie równą tożsamościowo zeru,która spełnia równanie funkcyjne f{xi)'f(x₂) =/(*! - x₂), dla każdego x_lt x₂eR.

2.4. Dane są funkcje g:R+ -* R+,p :R+ -» R określone wzorami g(x) = x³ i p(x) = log_a x.

9