DSCN1110 (2)

2.27. Wskazówka. Rozwiązując układ [W(p) = q | W(q) = p.

otrzymujemy równanie:

p² + (ą — 9 )p + q² — 9q — 1 = 0, gdzie

4 = -3 q² + 18 q + 85 Łatwo zauważyć, że dla q = 1 jest 4 = 100, a stąd

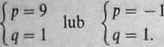
Warunkiem koniecznym istnienia par p, q spełniających warunki zadania jest by 4 była pełnym kwadratem.

Metodą prób można znaleźć wszystkie pary, o których mowa w zadaniu, np. dla q = —3, 4 = 4, q= -2, 4 = 37, q=-l 4 = 64,

gdzie

qe{-3, -2, -1,0.....9}.

Rozwiązaniami są:

	-3	-2	-1	0	1	2	3	4	5	6	7	8	9
4	4	37	64	85	100	109	112	109	100	85	64	27	4

2.28. Niech W{x) - a₀ + a_tx + a₂x² + ... + a„x".

Wobec tego

{a₀ + 2u y + 4a₂ +... + 2 ⁿa_n — 7 \ a₀ + 5a, + 25a₂ + _ + 5"fl„ = 13.

Odejmując równania stronami, otrzymujemy

(1) 3a, + 21a₂ + 117a₃ +... + (5" - 2") a„ = 6.

Można wykazać, że A 3|(5--2").

ifif

Wobec tego dzieląc obie strony równania przez 3 otrzymujemy /5" - 2"\

a, + la₂ + 39a₃ + ... + (—-—\a_H = 2.

Obierając dowolnie a₂, a₃, ..., a_n(a_n =£0) z równania (l) wyznaczamy a,.

Następnie z jednego z danych równań wyznaczamy a₀, czyli

_flo=7-1 m * = 1 -■

i otrzymujemy wielomian n-tego stopnia.

Wielomiany, o których mowa w zadaniu, mają postać:

W_x (x) = 15 - 5x + x²,

W₂ (x) = 23 — 2x —■ 5x² 4- x³.

Rozwiązanie drugie.

W_n(x)=W_n_₂(x)(x-2)(x-5) + ax + b, st. W_n_₂ = n- 2, W_n( 2) = 2a + b = l,

W„( 5) = 5n 4- b = 13,

3a = 6,    -7 kósttfof

a = 2 6 = 3,

czyli H^(x) =    ₂(x) (x - 2) (x - 5) + 2x + 3.,

2.29. Niech W(x) = a₀ + a,x + a₂x² 4-... 4- a„x".

Z warunku VP(0) = 2 otrzymujemy a₀ = Z Ale

W{0) = W(x — x) = |® + *T(-x) - 2x² - 2, więc

(1)    W(x) + W(—x) = 2x² + 4 dla każdego xeR.

Ponieważ

iy(x) = n₀ + a, x 4- a₂x² 4-... + a„x",

W'(-x) = a₀ — a,x + a₂x² “ ^a3*³ + - + (“* O^-*.,*"• więc do.dając stronami otrzymujemy:

(2)    W{x) + W(-x)-2a₀ + la₂x² 4- 2a₄x⁴ 4-... + 2a_2kx^2k. Porównując (1) i (2), mamy

a₂ = 1 i a₄ = a₆ = ... = a_2k = 0.

Tak więc W może mieć następującą postać:

(3) W(x) = 24■ flj x + x² + a₃x³ 4- a₅x⁵ 4-... 4- ^2* +1Jfp⁺1 • ale z warunków zadania mamy

W(x + 1) = W(x) 4- W(l) + 2x - 2, wobec tego powracając do (3) otrzymujemy:

77