DSCN1165 (2)

b) Wskazówka. Przyjmując a = 2 , b

zauważmy, ze

fl²^ = 2¹

,b²^<7⁵.

Stąd b < a.

7.9. Wskazówka. Ponieważ 98 = 2 • 7², 56 = 7 • 2³, więc

log₉₈56 =

stąd log₇14 = b) log₅₄24 =

3 gf log₂7 1121og₂71 P + 2

3-p’

3-q

log₇14 =

1 + log₂7 log₂7 *

5q-r

c) log₂₇₅6655 =

2 + 2 r

7.10.    Wskazówka. Skorzystać z tożsamości

logJb Ą -, dla a, beR₊\{ 1}.

log_ba

7.11.    a) Wskazówka. Najpierw przedstawić daną liczbę w postaci

9    •    • ‘    ' %

log₂5 +-, a następnie oszacować ją. Szukaną liczbą cał-

l°g₂5 kowitą jest 6. b) 4.

(^b_±K)

^+k\a + k)^y

7.12.    Przy podanych założeniach prawdziwa jest nierówność

b 6 + fc _ b ,

- > —r. Stąd log.- > log, a a + k    a

> log,

~. m

czyli log^h - 1 > log_a+k(b + k) - 1.

Zatem log_ab > log_a+_k{b + k).

7.13.    Wskazówka. Najpierw zauważyć, że dana nierówność jest

równoważna nierówności Jk+l

L > l.

rr

(n + 1)*'

Następnie rozważyć funkcję /: <k; + oo)->R określoną wzorem

/(*) = ;

Tj i wykazać, że jest to funkcja rosnąca. Teraz

(x + 1)*

wystarczy dowieść metodą indukcji, że/(/c) > 1 dla ke Ni k > 3.

7.14.    Ponieważ mianowniki ułamków, występujących w danej nierówności, są dodatnie dla każdego x,yeR, więc możemy obie strony nierówności pomnożyć przez wspólny mianownik. Otrzymamy wtedy nierówność:

1)    \x + y|(l + |x|)(l + |y|) jlff + \x + y|)(l + |y|) + |y|(l +

+ \x + y\)(l + \x\).

Po przekształceniach nierówność 1) przyjmuje postać

2)    |x + y|< |x| + |y| + |xy| (2 + \x + y\), która jest równoważna danej nierówności.

Wiadomo, że \x 4- y\ < |x| + |y|. Ponadto |xy| (2 -f \x + y\) > 0. Wobec tego \x + y\< |x| + |y| + |xy|(2 + |x + y\).

Zatem nierówność 2) jest prawdziwa dla dowolnych x, yeR, a więc jest również prawdziwa dana nierówność.

7.15.    Wskazówka. Przekształcając daną nierówność wykazać, że jest ona równoważna nierówności

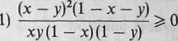
Następnie dowieść, że jeśli x, y spełniają podane warunki, to nierówność 1) jest prawdziwa.

7.16. Wskazówka. Skorzystaj z nierówności

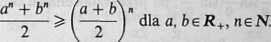
(patrz zadanie 3.5).

7.17. Najpierw rozważmy funkcję/: (0;-n) -> R określoną wzorem

/(x) = sinx + tgx — 2x.

Funkcja /jest ciągła i różniczkowalna, przy czym

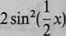
f'(x) = cos x H---? --—(1 + cosx — cos²x).

Ponieważ f\x) > 0, więc funkcja /jest rosnąca. Ale

*-o+

lim f(x) = 0, zatem f(x) > 0 dla każdego xe(0; \tc). Stąd teza. *-*<>+ 2

187