fizyka007

Ruc mend}

Definicje prędkości i przyspieszenia. Wektory prędkości » i przyspieszenia a punktu materialnego poruszającego się w przestrzeni definiujemy następująco

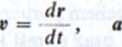
dv

dt

(2.1)

gdzie r — wektor położenia punktu (zob. rys. 1-1), którego składowe w kartezjańskim układzie współrzędnych prostokątnych wynoszą x, y, z. Zatem składowe wektorów t> i a względem osi tego układu wyrażają się wzorami

dx	dy	dz	(2.2a)
^: dt ’	°’ = 7T-	^D-" di
dvx	do.	dv.	(2.2b)
dt ’	^a’ -•	_ X ^a‘ ^= W

a długości wektorów v i a, oznaczane przez v i a lub przez |r| i |a| są dane wzorami

v *> }/v\ + o, + v] , a = Val+a} + af    (2.3)

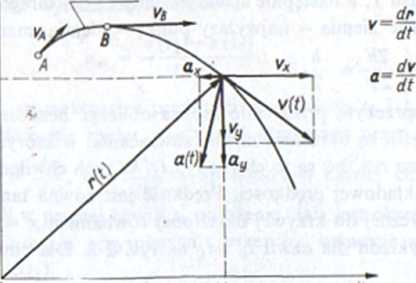
Wektory prędkości i przyspieszenia określone wzorami (2.1) są więc odpowiednio szybkością zmiany wektora położenia (jego wartości i kierunku) w czasie oraz szybkością zmiany wektora prędkości w czasie. Z definicji (2.1) wynika, że wektor prędkości jest w każdej chwili ruchu styczny do toru. Na rysunku 2-1 wektory v_A i v_B oznaczają prędkości w punktach A i B; są one styczne do toru. W ruchu krzywoliniowym wektor przyspieszenia nie jest styczny do toru.

Zapis kinematycznego równania ruchu, to znaczy postać funkcji r = — r (/) zależy od przyjętego układu współrzędnych. Dla ruchu na płaszczyźnie (rys. 2-1), składowe wektorów r, r, a w przyjętym układzie współrzędnych są funkcjami czasu i odpowiednio wynoszą: *(/) i y(t) dla wektora r (f), v_x{t) i v,(t) dla wektora r (/) oraz a_x(t) i a_y(t) dla wektora a (/).

Kinematyczne równania ruchu prostoliniowego. W przypadku ruchu prostoliniowego, układ współrzędnych wybieramy tak, aby jedna z osi, na przykład oś Ox, pokrywała się z kierunkiem ruchu. Wówczas kinematyczne równanie ruchu przyjmuje postać tylko jednej funkcji czasu x = x (t). Znajomość tej funkcji pozwala określić bezpośrednio takie

o

y(t)

x(t)

X

Rys. 2-1

parametry ruchu, jak: położenie ciała w każdej chwili przez podanie współrzędnej x(t), odległość \x (t₂)-x (/_t)| między położeniami ciała w dowolnych dwu chwilach /, i f₂, drogę przebytą przez ciało, prędkość średnią i inne, a za pomocą wzorów (2.2) także prędkość i przyspieszenie w dowolnym punkcie.

Jeżeli w chwili /, ciało zajmuje położenie x(/_t), a w chwili t₂ położenie x(t₂), to jego prędkość średnia w przedziale czasu <f_lt f₂> jest określona wzorem

x(/₂)-x(r,)

(2.4)

Tak zdefiniowana prędkość średnia jest składową wektora prędkości średniej, przy czym znak tej składowej, a więc i zwrot wektora prędkości średniej na osi Ox zależy od znaku wyrażenia * (f₂)-x (fj). Jeżeli w szczególności położenia początkowe i końcowe ciała pokrywają się (ciało powróciło do położenia wyjściowego), wówczas v_if = 0. Prędkości średniej określonej wzorem (2.4) nic należy mylić ze średnią wartością (bezwzględną) prędkości

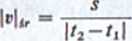
(2.5)

która w ogólności nie musi być równa prędkości średniej. We wzorze (2.5) oznacza całkowitą drogę przebytą w ciągu czasu \t₂ — f₂|.

i' 19