MG!74

Natomiast moduł Younga i współczynnik Poissona w funkcji modułu Kirchhoffa i modułu Helmholtza przedstawione są zależnościami

E= ^9BG m ^3B~^2G

3fl + G* ^V " 2(3B + G)'

4.1.2. Wyznaczanie stałych sprężystych materiału izotropowego

Celem ćwiczenia jest wyznaczenie technicznych stałych materiałowych badanego ośrodka izotropowego, tzn. modułu sprężystości podłużnej E (modułu Younga), współczynnika Poissona v, modułu sprężystości postaciowej G (modułu Kirchhoffa) oraz modułu sprężystości objętościowej (ściśliwości) B (modułu Helmholtza).

Ćwiczenie umożliwia również opanowanie techniki pomiaru z zastosowaniem. tensometrii elektrooporowej oraz obsługi uniwersalnej maszyny wytrzymałościowej.

4.1.2.1. Analiza teoretyczna

Podstawowe obliczenia wytrzymałościowe konstrukcji inżynierskich prowadzi się na ogół przy założeniu sprężystego zachowania się materiału, z którego rozpatrywana konstrukcja jest wykonana. Stosowane w obliczeniach związki konstytutywne, wiążące stan naprężenia ze stanem odkształcenia, wymagają doświadczalnego wyznaczenia występujących w nich technicznych stałych materiałowch.

Jak wiadomo, jednoznaczne określenie związków między naprężeniem a odkształceniem materiału izotropowego wymaga doświadczalnego wyznaczenia dwu niezależnych technicznych stałych materiałowych z czterech poprzednio wymienionych (£, v, G, B). Pozostałe dwie stałe można obliczyć ze związków wiążących jednoznacznie je parami między sobą. To, które z tych stałych zostaną uznane za niezależne, a które jako zależne, wynika ze stosowanej techniki pomiarowej przy ich wyznaczaniu.

W przeprowadzanych w trakcie ćwiczeń badaniach zostanie wyznaczony doświadczalnie moduł sprężystości podłużnej E i współczynnik Poissona v. Moduł sprężystości postaciowej G i moduł sprężystości objętościowej B będzie obliczony przy wykorzystaniu znanych już poprzednio stałych technicznych tzn. E i v.

1. W przypadku prostego rozciągania moduł sprężystości podłużnej E jest

współczynnikiem proporcjonalności w zależności

o_n = o = Et_w [MPa],    (4.38)

fi* s o - naprężenie normalne,

- względne liniowe odkształcenie wzdłużne (wzdłuż kierunku działającego naprężenia).

^ przypadku prostego rozciągania współczynnik Poissona wiąże odkształ-2' liniowe materiału

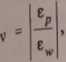
(4.39)

gdzie:

e - względne liniowe odkształcenie poprzeczne (w kierunku normalnym do kierunku działającego naprężenia).

y przypadku czystego ścinania moduł sprężystości postaciowej G jest współczynnikiem proporcjonalności w zależności

_0/ = t =    Gy [MPa],    (4.40)

gdzie:

o - x - naprężenie styczne,

Y - kąt odkształcenia postaciowego.

Moduł sprężystości postaciowej G w funkcji E i v wyraża się wzorem

G L    [MPa].    (4.41)

2(1 + v)

4, W przypadku czystego hydrostatycznego stanu naprężenia moduł sprężystości objętościowej jest współczynnikiem proporcjonalności w zależności

p = Btl    [MPa],    (4-42)

gdzie:

p - ciśnienie hydrostatyczne (p = oj,

0 - względne odkształcenie objętościowe EV/V.

Moduł sprężystości objętościowej B w funkcji E i v przedstawia zależność

B • —-— [MPal.    (4.43)

3(1 -2v)

4.1.2.2. Analiza doświadczalna

W szczękach maszyny wytrzymałościowej jest zamocowana płaska próbka z materiału izotropowego z naklejonymi tensometrami wzdłuż kierunku rozciągania (wzdłużny) T_w i poprzecznie do kierunku rozciągania (poprzecz-

109