3226794617

6. DZIAŁANIA NA MACIERZACH

DZIAŁANIE + własności

PRZYKŁAD

Dodawanie macierzy - dodajemy odpowiednie elementy macierzy równych wymiarów.

A + B = B + A

(A + B) + C = A + (B + C) (A+B)^T = A^T + B^T

Mnożenie macierzy przez liczbę -

- mnożymy przez daną liczbę wszystkie elementy tej macierzy.

k-A=Ak oraz | k- An| — kⁿ • IA | k-{A + B) = k-A + k-B w-(k-A) = (w k) - A (w + k)A = w-A + k-A

Mnożenie macierzy - mnożymy odpowiednie kolumny pierwszej macierzy z kolejnymi wszystkimi wierszami drugiej.

A B^B A

A-J = J-A = A (A ■ B) • C = A • (B-C)

A-(B+ C)= A-B +A-C k- (A-B) = (k-A) -B = A- (k-B)

(A • B)^T = B ^T • A^T

Am*n + B m*n — B m_xn + Amji

b 1 , T e f 9 h

[■c51±

a±e b±f c ± g d±h.

1 2		1 3		1+1 2 + 3'		2 5
0 1	+	0 0	=	0+0 1+0	=	0 1
1 2 .		.0 3.		. 1 + 0 2 + 3.		.1 5.

k-A = k-ctij - ctit * k-B

ka kb

r a b i _ r ka kb ] l c d \ ~ i kc kd\

r i 0 j	|_f^31	3- 0 '	l-f^3	^0 1
12 3 J	1 13 - 2	3- 3 .	1 1.6	9 J

Am*k • Bk*n — Cm-jt

C = Clii-bi\ + Cli2'bi2 +... + CLij-bij — C ij

r«i	«2	^a3 I	Ci	dl f
U	bz	-12x3	Cl C3	^2 d3J

3x2

ćllCi + CI2C2 + Cl₃C₃ O^idi + (^2^2 "ł" ^3^3

biCi + b₂c₂ + Z?₃c₃ b₁d_l + b₂d₂ + ^3^3

J2x2

Przykłady mnożenia macierzy:

0 1 + 1

21 + 1

0 • 2 + 1 • 0 2-2 + 1-0

-1

5

1 • 6 + 3 • 2 + 2 • (-1)

(-2)-6 + (-1) ■ 2 + 0 • (-1) 4-6 +0-2 + (-3) ■ (-1)

1	1 • 2 + (-3) • 0 .		6
	6 + 6-2		10
=	-12-2 + 0	=	-14
	.24 + 0 + 3 .		. 27 .

[° ^1 2 X • 1 -3		^3 1 L-i i
1	3	2
-2	-1	0
. 4	0	-3 .

6

2

-1

0 3 + 1 (-1) 2*3 + l-(-l)

L 1 • 3 + (-3) • (-1)

7. MACIERZ ORTOGONALNA

Macierz ortogonalna = macierz transportowana i odwrotna do niej są identyczne.

R^t=R-' a RR^t = RR'=J a det R = ±1

Iloczyn macierzy ortogonalnych jest macierzą ortogonalną.

(R_i R₂)-(R, R₂)^t = R| R₂- R₂^t R,^t = R, J r,^t= r, r,^t= j

Suma iloczynów wszystkich odpowiadających sobie k-elementów dwóch różnych wierszy oraz dwóch różnych kolumn = 0. Suma kwadratów elementów dowolnej kolumny i dowolnego wiersza = 1.

n

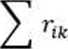
ij=1

n

ij= 1

oraz

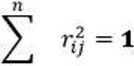
i— 1 v /'= 1

© Copyright by Iiwa Kędzi orczyk

-64-

w w »v. ma tein utyka. sosno wiec.p I