3226794658

7. PODOBIEŃSTWO I PRZYSTAWANIE A. Fiflury..Rpdp.bne

Figury podobne zachowują rozwartości odpowiednich kątów oraz stosunki odpowiednich boków. Stosunki odpowiednich boków figury F do odpowiednich boków figury podobnej F^/ są stałe (nazywamy je skalą podobieństwa). Skała podobieństwa (k) decyduje ile razy figura F' została powiększona lub pomniejszona w stosunku do figury F.

Figury podobne są więc proporcjonalnie powiększone lub pomniejszone w stosunku do siebie.

Podobieństwo figury F' do figury F oznaczamy:    F' ~ F

Przykłady podobieństwa: Wszystkie kwadraty są do siebie podobne, wszystkie romby są podobne, wszystkie trójkąty rówmoboczne są podobne, wszystkie koła są do siebie podobne. Nie wszystkie prostokąty są do siebie podobne.

Własności podobieństwa:

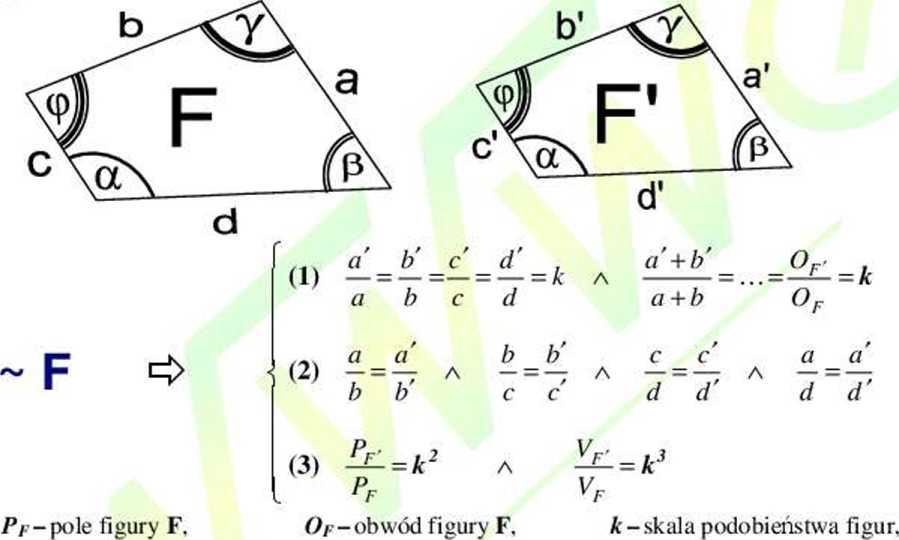
dla:

B. Fi.aH.r.y..E.r?y.S.t.ąi.ąc.e

Figury przystające są to figury podobne o skali k = 1. Zachowują one rozwartości odpowiednich kątów oraz długości odpow iednich boków (więc również stosunki odpowiednich boków).

Figury przystające są więc identyczne (można je na siebie nałożyć). Powstają one w wyniku przekształceń izometrycznych (patrz, przekształcenia płaszczyzny i przestrzeni).

8. TWIERDZENIE TAL ES A

Dotyczy proporcjonalności odpowiednich odcinków powstałych w wyniku przecięcia kąta prostymi równoległymi.

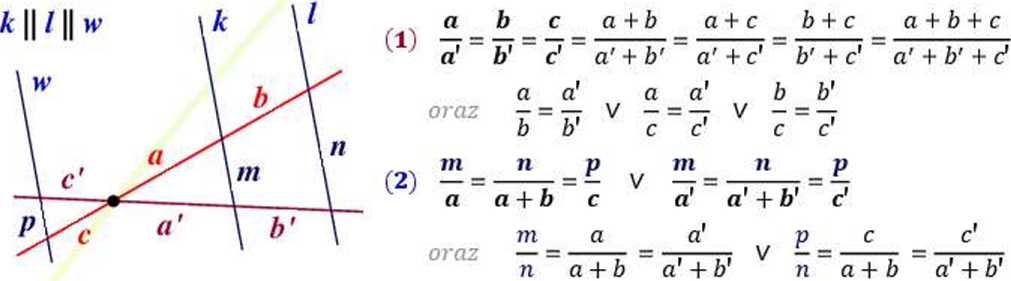
W wyniku przecięcia kąta prostymi równoległymi otrzymujemy trójkąty podobne.

© Copyright by Ewa Kędziorczyk    - 282 -    www.matematyka.sosnowiec.pl