figury podobne A

FIGURY PODOBNE

GRUPA A

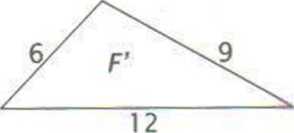
1. Skala podobieństwa trójkąta F do trójkąta F wynosi:

A. i    C. 6

B. 3    D. 9

²ZtA

4

2. Odcinki c i b są proporcjonalne do odcinków a i d. Zatem prawdziwa jest równość:

A.

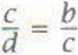
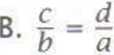
_r c _ b '-'a-d

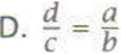
3. Które dwa z podanych prostokątów⁷ są podobne?

A	2	B	4	C
4				3

A. B i C B. A i B C. A i C D. nie ma prostokątów podobnych

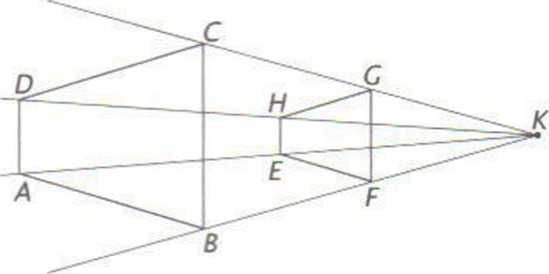
4. Czworokąty' ABCD i EFGH na rysunku poniżej są jednokladne. Środkiem jednokładności jest: A. czworokąt EFGH B. punkt K C. czworokąt ABCD D. punkt F

5.    Pewne dwa prostokąty są podobne w skali 3 : 4. Stosunek ich pól wynosi:

A.j B.1 C. 12    D.$

6.    Boki trójkąta ABC mają długości 4cm, 5cm, 6cm. Boki trójkąta podobnego A'B C w skali \ maj długości:

A. 2 cm, 2,5 cm, 3 cm B. 8 cm, 10 cm, 12 cm C. 2 cm, 5 cm, 6 cm D. 8 cm, 5 cm, 6 cm

7.    Dany odcinek podziel konstrukcyjnie w stosunku 1 : 2.

8.    Nakreśl odcinek AB i zaznacz punkt 5 leżący poza odcinkiem AB. Skonstruuj odcinek A'B' jednokładn do AB względem punktu 5 w skali

9.    Zbuduj odcinek x tak, aby zachodziła zależność ^    |.

ab    c

■-1 ■ •---¹

10.    Trójkąt prostokątny ABC o przyprostokątnych 3 cm i 4 cm iest podobny do trójkąta AB'C, którego obwód wynosi 36 cm. Oblicz długości boków trójkąta A'B’C.

11.    Uzasadnij, że odcinek łączący środki dwóch boków trójkąta jest równoległy do trzeciego boku i równy jego połowie.

1

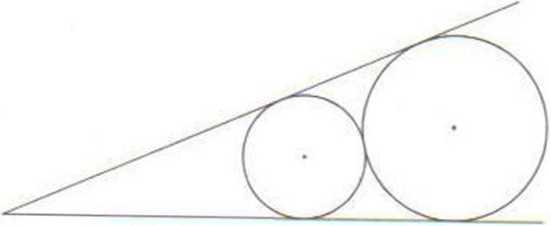
12. Odległość między środkami okręgów stycznych zewnętrznie i stycznych do ramion kąta jest równa 10 cm.

Odległość środka mniejszego okręgu od wierzchołka kąta jest równa 20 cm. Oblicz długości promieni tych okręgów.