6355787052

Z. Rudnicki: MATLAB - KOMPENDIUM

Iogl0(x)	logarytm o podst 10_1
sign(x)	znak x
mod(x)	reszta z dzielenia
sin(x), cos(x), tan(x), cot(x)	funkcje trygonometryczne ]
sinh(x), cosh(x), tanh(x). coth(x)	funkcje hiperboliczne
asin(x), acos(x), atan(x), acot(x)	f. odwrotne do trygonometrycznych
round(x)	zaokrągla do najbliższej całkowitej
ceil(x)	zaokrąglenie w górę (dosłownie: sufit)
fix(x)	zaokrągla w stronę zera
floor(x)	zaokrągla w dół (dosłownie: podłoga)
imag(x)_	część urojona liczby zespolonej
real(x)_	część rzeczywista liczby zespolonej_
gcd(x)_	największy wspólny podzielnik
[ lcm(x)	najmniejsza wspólna wielokrotność

Wykaz funkcji elementarnych można uzyskać wpisując: help elfun

2.1.7. Ćwiczenia - obliczenia kalkulatorowe

Sprawdź w Matlabie poprawność obliczeń:

3,87 10⁵ - 72,86³

2--J2

= 370,255 _oblicz: 7,7³

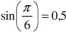
Zastosuj tzw. „notację naukową” zapisu liczb w obliczaniu:

1,78 10'⁴ +9,76" 128000000

+ 0,00005 =

2.1.8. Ćwiczenie - obliczenia z użyciem zmiennych

2 6

Oblicz wartość zmiennej: ^    _ ą x² —5x

dla x = 8,167 oraz x =-8,167 (Powinno być: 0,748 i 0,924)

2.1.9. Relacje i wyrażenia logiczne

Wyrażenia logiczne umożliwiają sprawdzanie prawdziwości określonych zależności dla konkretnych danych liczbowych. Najprostszymi wyrażeniami logicznymi są relacje. Relacja to dwa wyrażenia arytmetyczne połączone operatorem relacji. Używane w Matlabie operatory relacji podaje Tabela 2.1. Tabela 2.1. Operatory relacji

Operator	Znaczenie
<	mniejsze
<=	mniejsze lub równe
>	większe
>=	większe lub równe
==	równe
~=	nierówne (w FreeMat jest: != )

Przykłady relacji:_

| x>5, b*b-4*a*c>=0, 5==x^A2+y, 2*(m-3*h)*2<=sqrt(u^A2+5*h), x+a>x    |

Wartości logiczne tych relacji Matlab może wyznaczyć dopiero gdy:

a)    będą znane wartości liczbowe wszystkich występujących w nich zmiennych,

b)    zostaną obliczone wartości liczbowe wyrażeń arytmetycznych.

Sprawdź w oknie komend wybrane relacje, nadając wcześniej wartości występującym w nich zmiennym.

W Matlabie nie ma osobnego typu dla stałych i zmiennych logicznych ponieważ ich rolę pełnią stałe, zmienne i wyrażenia arytmetyczne. Wartość liczbowa zero jest bowiem traktowana jako wartość logiczna "fałsz" natomiast wartości liczbowe różne od zera są utożsamiane z wartością logiczną "prawda". Także odwrotnie - wszystkie prawdziwe relacje i wyrażenia logiczne mają wartość liczbową 1 a fałszywe mają wartość zero.

10