19583

1. Zbadać typ zbieżności (warunkowa, bezwzględna) szeregu: ^ (-1)'

nm\

(*!)V

(2/7)!

2.    Wyznaczyć przedziały monotoniczności i ekstrema funkcji: f(x) = x ■ e^x.

3.    Metodą współczynnika Lagrange’a wyznaczyć ekstrema funkcji f(x,y) = x² + 2y* - xy, przy warunku 2x + y = 22.

4. Obliczyć pole obszaru ograniczonego krzywymi: y - y ”    ^{x e<} >

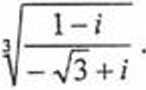
5.    Wyznaczyć

6.    Sformułować definicję granicy: lim f(x) = g.

3*.

1.    Wyznaczyć przedziały wklęsłości i wypukłości funkcji: /(*) _{= e}4

2.    Zbadać zbieżność szeregu: Ź(-l)"(^~)"’. Sformułować zastosowane kryterium

3.    Wyznaczyć ekstrema warunkowe funkcji f(x,y) = 4 - x + 2y, gdy x² + 2y* = 12.

4.    Obliczyć:    .

5.    Rozwiązać równanie różniczkowe: x y’ = y (lny — lnx).

6.    Wyznaczyć asymptoty funkcji: f(x) = ln x--—

x-5