2070

Twierdzenie (WK zbieżności szeregu)

1) X /„ jest zbieżny punktowo (bezwzględnie) =>    /„ ^*0 , tzn. funkcją graniczną

„=i    "~®

ciągu (f„)_MN jest funkcja /= 0

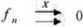
«-"CC

2) X/» jest zbieżny jednostajnie =»

M-l

Twierdzenie (WKW Cauchy’ego zbieżności szeregu funkcyjnego)

Niech X -zbiór

(r ,||-||) - przestrzeń Banacha oraz niech

f„:X-Y dla «eN.

Wtedy

X /*(*’

1) X/« - zbieżny punktowo na X <=■ V.veX Vr>0 3n₀ Vn>m>«₀

2) X/.

W“ I

- zbieżny jednostajnie na X <=> Vf>0 3w₀ V/i>m>n₀

X /.w

k=m

<£

Twierdzenie (kryterium Weierstrassa)

Niech A^- -zbiór

(y.ll-llj - przestrzeń Banacha oraz niech

f„:X-Y dla «elN

Jeśli

to

VneN \/*eX j|/„(.r)||so„ oraz X a„-szereg zbieżny, X /„-zbieżny bezwzględnie i jednostajnie.

Dowód

1) Sprawdzamy WKW Cauchy'ego zbieżności jednostajnej:

X fk(x

Vf>0 3m„ Vn>m>n„ V.reAf

-2-