25851

jest lewostronnie ciągła w punkcie x₀ wtedy i tylko wtedy, gdy

lim f(x) = fOo)

Uwaga. Podobnie wygląda definicja ciągłości lewostronnej funkcji f ■ (o, b] —» R , gdzie -oo<a<b < oo, w punkcie x₀e (a,b]. Analogicznie definiuje się funkcję prawostronnie ciągłą w punkcie.

Tw. 3.1.6 (warunek konieczny i wystarczający ciągłości)

Niech funkcja f będzie określona na przedziale (a,b), -oo<a<b<oo oraz niech x₀ e (a,b). Funkcja f jest ciągła w punkcie xo wtedy i tylko wtedy, gdy jest lewostronnie i prawostronnie ciągła w tym punkcie.

Del. 3.1.7 (funkcja ciągła na przedziale)

Funkcja f jest ciągła na przedziale, jeżeli jest ciągła w każdym punkcie tego przedziału.

Uwaga. Ciągłość funkcji na przedziale [a,b] oznacza jej ciągłość w każdym punkcie przedziału otwartego oraz prawostronną ciągłość w punkcie a i lewostronną ciągłość w punkcie b. Analogicznie można zdefiniować ciągłość funkcji na sumie przedziałów lub na bardziej skomplikowanych podzbiorach prostej.

3.2 NIECIĄGŁOŚCI

Del. 3.2.1 (nieciągłości pierw szego roil/aju)

Niech funkcja /"będzie określona na przedziale (a,b), -<» < a < b <, <» oraz niech xo e (a,b). Funkcja f ma w punkcie xo nieciągłość pierwszego rodzaju, jeżeli istnieją granice skończone

lim f(x), lim f(x)

*-»*o    *-**i

oraz

lim\f(x)*f(x„)    _lub lim f(x)* f(x₀)

x-»*_#    *-**«

Uwaga. Mówimy, że funkcja f ma w punkcie xo nieciągłość pierwszego rodzaju typu „skok”, jeżeli spełnia warunek

lim f(x) * lim f(x)

*~**i    *-+*i

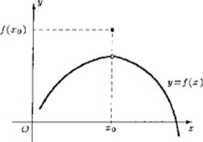
Natomiast, jeżeli funkcja/"spełnia warunek

lim f(x)= lim f(x)* f(x₀)

X-**i    X-*Xj    '

to mówimy, że ma ona w punkcie xo nieciągłość pierwszego rodzaju typu „luka”.

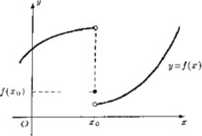
Rys. 3.2.1 Funkcja /"ma w punkcie xo

Rys. 3.2.2 Funkcja f ma w punkcie Xo