65005 img454 (2)

Zatem funkcja ta będzie ciągła w punkcie x₀ = 3, jeśli 3a + b - O. Dalej mamy

lim    3)

h

lim I—~ (³⁺^)²l ~ O

h^o-    _h

- lim

h-*o~

-V (6+b)

!

=-6=.nii

Ponadto:

lim    ..    [g(3+6)+b]-0 _ , ah + 3o + 6

^°⁺    h    ~h™o⁺    _h    -    h

Wiemy, że 3a + b = 0 (z warunku ciągłości). Wykorzystując ten fakt w osin! niej granicy, mamy

lim

/>-> o

+

ah + 3a + b h

nh1

= lim . ~ = a =    3),

/i->0⁺    J +v '

zatem aby funkcja była różniczkowalna w omawianym punkcie, musi być a- (>

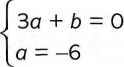
, którego rozwiązaniem jen

Otrzymaliśmy więc układ równań [a = - 6

6=18

para liczb

Tak więc dla a — 6 i b = 18 nasza funkcja jest ciągła i różniczkowalna w punkcie x₀ = 3.

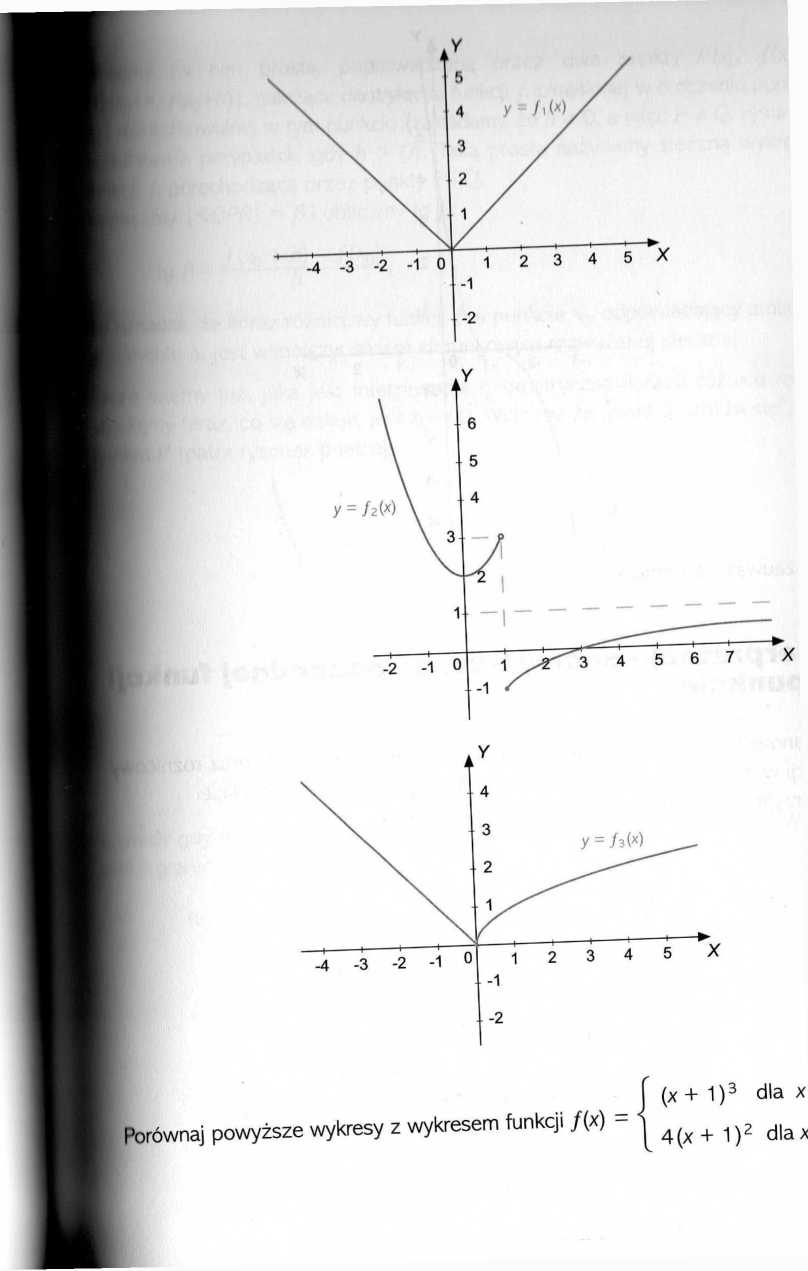
Nasuwa się pytanie, czy można poznać na podstawie wykresu funkcji, że funkcja (określona w otoczeniu tego punktu) nie jest różniczkowalna w tym punkcie. Otóż analizując wykresy funkcji

/iM = l*|,

x² + 2

f₂(x) =< X- 3 I x+ 1

dla x < 1

„    . . oraz/₃(x) -

dla x > 1    '

-x dla x < 0 4x dlax>0

zauważamy, że funkcja nie jest różniczkowalna w punktach, w których, albo nie jest ciągła, albo (jeśli jest ciągła) jej wykres ma tzw. ostrza (linia nie przebiega gładko, lecz „się załamuje”).