3582320732

3. FUNKCJE CIĄGŁE 3.1 CIĄGŁOŚĆ FUNKCJI

Def. 3.1.1 (funkcja ciągła w punkcie)

Niech funkcja f będzie określona na przedziale (a,b), -oo < a < b < oo oraz niech xo e (a,b). Funkcja f jest ciągła w punkcie xo wtedy i tylko wtedy gdy

lim f(x) = f(x_Q)

x->x₀

Obrazowo, funkcja jest ciągła w punkcie, gdy jej wykres nie „przerywa" się w tym punkcie.

Def. 3.1.2 (Heinego funkcji ciągłej w punkcie)

Niech funkcja f będzie określona na przedziale (a,6), -oo < a < b < oo oraz niech xo e (a,b). Funkcja f jest ciągła w punkcie Xo wtedy i tylko wtedy, gdy

A [llim x    [lim f(x )= f(x₀)|]

(,y„)

{Y„}c(0,i))

Def. 3.1.3 (Cauchy^Jego funkcji ciągłej w punkcie)

Niech funkcja f będzie określona na przedziale (a,b), -oo < a < b < oo oraz niech Xo e (a,b). Funkcja f jest ciągła w punkcie xo wtedy i tylko wtedy, gdy

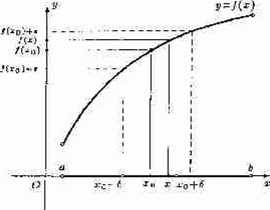
Rys. 3.1.2

Ilustracja definicji Heinego funkcji ciągłej w punkcie

Funkcja f jest ciągła w punkcie x_a gdy małe zmiany argumentu x względem punktu x₀ powodują małe zmiany wartości funkcji /(x) względem wartości f[xo).

Tw. 3.1.4 (o równoważności definicji ciągłości funkcji)

Definicje Heinego i Caucłr/ego ciągłości funkcji w punkcie są równoważne.

Def. 3.1.5 (funkcja lewostronnie ciągła w punkcie)

Niech funkcja f będzie określona na przedziale (a,ł>), ~°° < a < b < oo oraz niech xo e (a,b). Funkcja f