3582320735

2. GRANICE FUNKCJI

2.1 PODSTAWOWE OKREŚLENIA

Def. 2.1.1 (Heinego granicy właściwej funkcji w punkcie)

Niech funkcja f będzie określona na przedziale (a,b), -<» < a < b < ca, z wyjątkiem być może punktu xo g (a,b). Liczba g jest granicą właściwą funkcji f w punkcie xa co zapisujemy

lim f(x) — g

*-»*<, ¹

wtedy i tylko wtedy, gdy

lim f(x„) = g

A (■*.)

(x„ }c(a,b) _

' x_n & x₀ dla każdego ne N ^x limy, = x n

V"

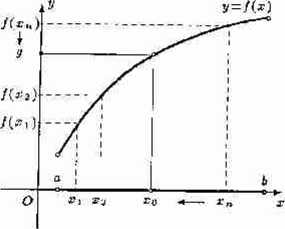
Rys. 2.1.1

Ilustracja definicji Heinego granicy właściwej funkcji w punkcie

Obrazowo, funkcja f ma w punkcie xo granicę właściwą g, gdy jej wartości odpowiadające argumentom dążącym do punktu xo (i różnym od tego punktu) dążą do liczby g (rys. 2.1.1)

Uwaga. Wartość funkcji f w punkcie Xo (o ile istnieje) nie ma wpływu na jej granicę w tym punkcie. Definicję granicy funkcji można podać także (bez większych zmian) dla funkcji określonych na sumie przedziałów otwartych, w punktach wewnętrznych przedziałów domkniętych itp. Zamiast

równości f(^x) ⁼ 9 można stosować także zapis f(^x) _x->x„ ^> 9, albo też    9, gdy ^x -» *₀.

Fakt 2.1.2 (o nieistnieniu granicy funkcji w punkcie)

Jeżeli

o oraz

1. hmx„'=x

lim f(x_n') = g'

2.    limx_n"= x_{0 oraz} lim f(x_n") = g"

n—>oa    n—>oo    ³

3.    g'*g",

to granica f(^x) nie istnieje (właściwa ani niewłaściwa).

Uwaga. Powyższy fakt jest prawdziwy także wtedy, gdy g’ = ± <x> lub g“ = ± oo.

Def. 2.1.3 (Cauchy’ego granicy właściwej funkcji w punkcie)

Niech funkcja f będzie określona na przedziale (a,6), -<*> < a< b< <», z wyjątkiem być może punktu x₀ g (a,b). Liczba g jest granicą właściwą funkcji f w punkcie Xa co zapisujemy

lim f(x) = g

wtedy i tylko wtedy, gdy