96082

Der. 1.1.2 (luki na płaszczyźnie)

a) Niech funkcja f :(<*,/£] -» R^: będzie ciągła i równowartościowa na przedziale laikiem zwykłym na płaszczyźnie nazywamy zbiór:

r =    £[<*,/?] .

Rys. 1.1.4 Luk zwykły na płaszczyźnie

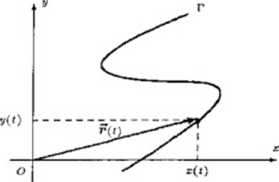
b) Niech funkcja r : I —» R^J, gdzie I oznacza dowolny odcinek, półprostą lub prostą (z końcem lub nic), będzie ciągła i lokalnie równowartościowa na L laikiem na płaszczyźnie nazywamy zbiór:

r= H(t):t<=i

Rys. 1.1.5 łoik na płaszczyźnie

c) Jeżeli dla łuku T = r^(t):t e[cr,/?] spełniona jest równość r(c*) = r(/?), to mówimy, że łuk ten jest zamknięty. W przeciwnym przypadku mówimy, że łuk 1 jest niezamknięty.

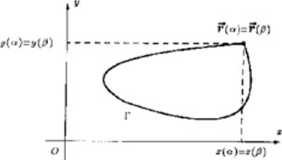
Rys. 1.1.6 Luk zamknięty na płaszczyźnie

d) Jeżeli funkcja r w definicji łuku zwykłego jest różniczkowało a w sposób ciągły na (a,P) oraz dla każdego t € [a,P\ spełniony jest warunek:

f(t)*Ó,

to mówimy, że łuk tai jest gładki. Mówimy, że łuk jest kawałkami gładki, jeżeli można go podzielić na skończoną liczbę łuków gładkich.

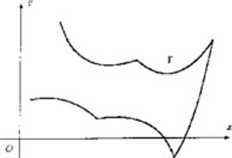
Rys. 1.1.7 Luk kawałkami gładki na płaszczyźnie