27895

snaia 2/8
Przestrzeń metrycza zupełna
Przestrzeń metiyczną X nazywamy zupełną, gdy każdy ciąg Cauchy’ego jej elementów jest zbieżny do pewnego jej elementu.
77. Własności ciągów zbieżnych, twierdzenie o średnich arytmetycznych, tw ierdzenie o średnich geometrycznych.
Własności ciągów zbieżnych:
1. Jeśli ciąg (Qn) jest ograniczony i () zbieżny do 0 to ( Q n ) *( Jjn ) jest zbieżny do 0.
2. Jeśli ciągi ( q ),( Jjn) są zbieżne (mają granicę) oraz istnieje 0 ' Q ~ b ’ ^ " No
3. Jeśli ciągi ( Qn ),( ) są zbieżne to zbieżne są ciągi (Qn l)n ).( Qn bn Qn *
n ) oraz (c* n ) c=const ponadto:
1'm(a,,±b,,) = lima,±limb„ Ma/b,,)=lima,,,|imb, Mc*b) = c,tonbn
Jeśli ponadto założymy, że
limb n ^ ^to ciąg(^^) jest zbieżny.
L
Twierdzenie o średnich arytmetycznych
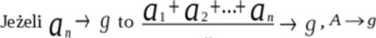
n
Tw. o średnich geometrycznych
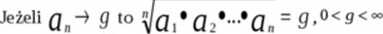
82. Kryteria zbieżności szeregów.
1. Porównawcze
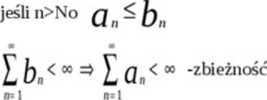
Wyszukiwarka
Podobne podstrony:
PRZESTRZENIE METRYCZNE ZUPEŁNE I NIEZUPEŁNE Definicja Przestrzeńmetryczną(X,d) nazywamy zupełną, gdy
Twierdzenie 1.6 £d jest przestrzenią metryczną zupełną.4 Definicja 1.2 Niech a, b 6 Rrf. Odcinkiem
Wykład 5 - Transformacje 3D Transformacja przestrzeni trójwymiarowej nazywamy przekształcenie L:R3
teoria2 2 Przestrzenią wektorową nazywamy strukturę: (V ,+, (R, +, *), *) + : V+V -> V *: R*
PMETR (X, d) - przestrze ń metiyczna K(x0 ,r) = (x e X, d(x, x0)<r} XdU- otwarty V 3 K (x, r
85213 str265 ROZDZIAŁ 5Zarys rachunku tensorowego§ 1. Pojęcie tensora Definicja 1. Przestrzenią abst
DSC00586 Wo/d/M* 2. ElMn^nły topologii 113 definicja normalności: Przestrzeń topologiczny X. nazywam
DSC00588 113 d#łuiU
przystosowawczą zapewnia ich dążność do przestrzegania tradycji. Nazywa ich „ludźmi sterowanymi
Zdj?cie0175 Poczytalność sprawców przestępstw seksualnych ■ Przeważający pogląd: Gdy przestępstwo se
więcej podobnych podstron