31142

(h) Określić równanie układu zatnkiięlep/.).

(b) W celu zbadania stabilności układu ranuu-ięiego II ir.ciod^ Lapunowa zdefiniowano fo-inę kwadrrtowo

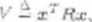
.wizie Tl £ 3t    . • katać warunki, które musi spełniać macierz Tl, aby .imkcja V mogła >ye jawtrzegana jzke propozycja,

ńinkcji Lagunowa.

(n) Wykazać, że pochodny po czasie fuaaeji opisanej równaniem (6) można przedstawić w postne: \' — —x~Qx, gdzie Q ^ R' ⁿ- Określi*' poste* ć macierzy Q biorąc pod uwagę definicję . :ikoj^; V oraz rówi aule zar/.kniętegu iik'adu regulacji. Podać, jakie właściwości musi spełniać macń rz Q, aby na podstawie V i l ’ wnioskować o asymptotycznej stabilności piu:kt.:i 0.

¹ J [Oruga metoda Łapanowa układ nieliniowy] Nn rysnn:<u 1 przedstawione układ nii-chaniczny w postaci wahadła mateniatycziiego o długości R i masie skupionej A/ umieszczonego w polu grawitacyjnym n przyspieszeniu y. Przyi<jć, żc w punkcie obrotu występuje tarcic prędkowstowe, którego współczynnik wynosi b.

b

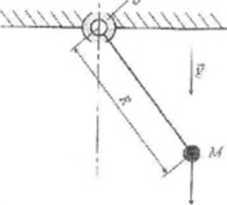
Rysunek I: Układ niechr.nic/uy do zacluuia 7

(a)    Napisać równanie dynamiki wahadła.

(b)    Podać propozycję funkcji La? inowa.

(c)    Sprawdzić wykorzystując II metodę Łapanowa czy układ jest asymptoiyr/.nie stabilny.

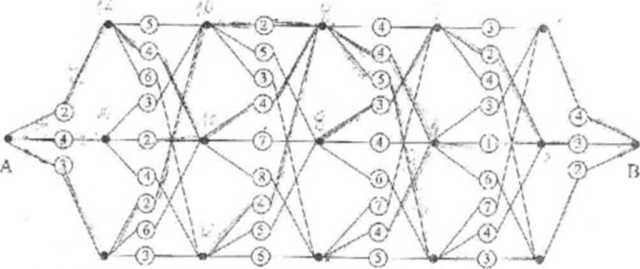
^ [Programowanie dynamiczne] Rozpatrzmy szcscioelapowy proces przeraz ounktu A uo B wzdłuż jednej z możliwych dn'»g datki (rys. 1). Decyzja wyboru drogi u> sterowanie +1 dla drogi położonej najwyżej. 0 dla drogi położonej w środku oraz -1 fila drogi położonej najniżej (w <buiym punkcie siar.ki;. W uólku oznaczono koszt przejścia od punktu dn .omletu.

{a) Podać przejście od A do B przy minimalnym koszcie całkowitym, r?) Narysować odpowiadai sygnał srcrująey.

; .•

c.

Rysunek 2: Graf do zwiania S

2