3526

Elektronika I rok zestaw 16

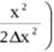
(funkcja Gaussa).

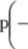
L Dana jest funkcja falowa w postaci: y(x) = Cex

Prawdopodobieństwo zaobserwowania pędu p dla układu reprezentowanego przez tą funkcję opisane jest funkcją gęstości:

P(p) =¥ J<p "'(X) \ł*.\)dx |‘ gdzie : <p(x) =Cexpf— jjest funkcją własną operatora pęda

Oblicz powyższy rozkład gęstości prawdopodobieństwa. W jaki sposób można potwierdzić, że zasada nieoznaczoności jest spełniona (skorzystać ze wzoru na gęstość prawdopodobieństwa znalezienia cząstki w punkcie xtj. P(x)=xp*(x)\ł<x)) ?

2

(Przypomnienie) Pokazać, że energia całkowita dla cząstki o masie m poruszającej się w

polu centralnym w polu centralnym wynosi: E =    ^    + V(r); gdzie: V(r)-energia

2 2mr

potencjalna, L-moment pędu.

2 (Irodow 5.33) Wypisać możliwe termy (stany elektronów przy sprzężeniu L-S) atomów, dla których konfiguracja niezapełnionej powłoki jest: a) np², b) np³.

4. (Irodow 5.16) Wypisać konfiguracje elektronowe i znaleźć podstawowy term atomów a) C i N b)S i Q. Konfiguracje elektronów tych atomów odpowiadają zabudowie powłok elektronowych w normalnej kolejności.

5. (Irodow 6.1) Odpowiednie momenty magnetyczne atomu wieloelektronowego można

wyznaczyć ze wzorów: p, = -^^BL - dla orbitalnego momentu pędu L= . L(Loraz

n

p_s = -2 S - dla spinus =_N/S(S -+-l)W. Za pomocą modelu wektorowego obliczyć

h

czynnik Landego "g", który służy do wyznaczania momentu magnetycznego p, = -g ^^B J

w kierunku całkowitym momentu pędu elektronów J = J(J -+-1)M . Wskazówka: zrzutować całkowity moment magnetyczny elektronów na kierunek wektora J.

6. Obliczyć czynnik Landego odpowiadający poziomowi podstawowemu ( ²Sw ) oraz najniższym stanom wzbudzonym ( ²Pi/2 oraz ²Pj^ ) dla atomu sodu (nNa).