123057

Przykład

Niech/:R'->R\ f(x, v) = (ary, x + y, ,t^; + y^!).

Wyznac2yć pochodną kierankową funkcji/w punkcie (xo, yo) =(2,1) w kierunku wyznaczonym przez wektor v = [-1,2]

Wersor v, równoległy do wektora v jest postaci

I v |

[-1.2]

'“TT"

-y/Ś 2y/5 5 ’ 5

zatem

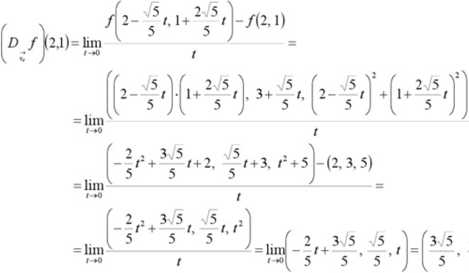
-(2. 3, 5)

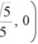
opracował Jacek Zaiiko