Całka oznaczona Riemanna
Niech f będzie funkcją określoną i ograniczoną w przedziale ![]()
.
Podział przedziału całkowania
Przedział ![]()
dzielimy na n przedziałów dowolnie wybranymi punktami a1, a2, ..., an-1 przy czym a=a0<a1<a2<...<an-1<an=b. Oznaczmy ten podział Pn .
![]()
długość przedziału ![]()
k=1,2,...n
Liczbę ![]()
nazywamy średnicą podziału Pn.
Suma całkowa
W każdym przedziale ![]()
wybieramy dowolnie punkt xk, obliczamy f(xk) i tworzymy sumę
![]()
(suma całkowa).
Def: Ciąg ![]()
podziałów przedziału ![]()
nazywamy normalnym ciągiem podziałów gdy ![]()
.
DEFINICJA
Jeżeli dla każdego normalnego ciągu podziałów przedziału ![]()
ciąg sum całkowych ![]()
( przy dowolnym wyborze argumentów) jest zbieżny do tej samej skończonej granicy, to tę granicę nazywamy całką oznaczoną (Riemanna) funkcji f w przedziale ![]()
i oznaczamy 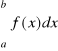
.
O funkcji f mówimy, że jest całkowalna w (sensie Riemanna) w ![]()
.
Zatem całka oznaczona jest liczbą.
Rozszerzenie znaczenia symbolu całki![]()
Jeśli
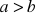
, to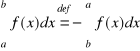
.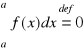
dla każdego a.
Wniosek
Jeżeli funkcja f jest nieujemna ![]()
w przedziale ![]()
, to 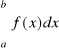
jest równa polu obszaru leżącego na płaszczyźnie Oxy między wykresem funkcji f i osią Ox w pasie ![]()
.
Warunki wystarczające całkowalności w sensie Riemanna
1. Funkcja ciągła w przedziale domkniętym jest całkowalna w tym przedziale.
2. Funkcja monotoniczna w przedziale domkniętym jest całkowalna w tym przedziale.
Modyfikacje funkcji niewpływające na istnienie i wartość całki.
TW. Jeśli
1 funkcje f i g są określone i ograniczone w ![]()
2 funkcja g przyjmuje wartości różne od wartości funkcji f w skończenie wielu punktach
3 f jest całkowalna w ![]()
to g jest całkowalna w ![]()
oraz 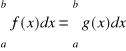
.
Uwaga
Funkcja nieograniczona w ![]()
nie jest w tym przedziale całkowalna.
Obliczanie całki oznaczonej za pomocą funkcji pierwotnej
Tw:
Jeśli funkcja f jest ciągła w ![]()
, a F jest dowolną funkcją pierwotną funkcji f w tym przedziale to
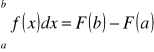
***
Piszemy krótko ![]()
Uwaga
Jeśli funkcja f jest ciągła w ![]()
to równość *** można przyjąć za definicję całki oznaczonej.
wzór na całkowanie przez części dla całki oznaczonej
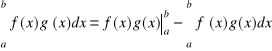
wzór na całkowanie przez podstawienie dla całki oznaczonej
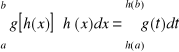
WŁASNOŚCI całki oznaczonej
Jeżeli funkcje f i g są całkowalne w przedziale ![]()
to
1. 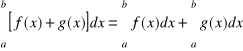
2. 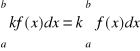
3.(o podziale przedziału całkowania)
Jeśli ![]()
, to 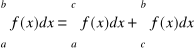
.
4. Jeśli dla każdego ![]()
spełniona jest nierówność ![]()
, to 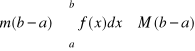
.
5. Jeśli dla każdego ![]()
![]()
, to 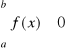
.
6. Jeśli dla każdego ![]()
![]()
, to 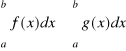
.
7. Twierdzenie (o wartości średniej) dowód
Jeśli f jest ciągła w ![]()
to istnieje punkt c, ![]()
taki, że 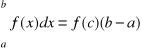
.
Def: Liczbę 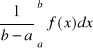
nazywamy średnią całkową funkcji f w przedziale ![]()
.
funkcjA górnej granicy całkowania
Niech f będzie funkcją całkowalną w przedziale ![]()
,zaś α dowolnie ustaloną liczbą w tym przedziale.
Def:
Funkcję
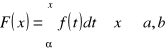
nazywamy funkcją górnej granicy całkowania całki.
Tw: dowód
Jeśli f jest funkcją całkowalną w ![]()
i ![]()
, to funkcja
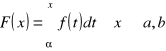
jest ciągła w przedziale ![]()
oraz ma pochodną ![]()
w każdym punkcie x, w którym funkcja podcałkowa f jest ciągła przy czym zachodzi równość ![]()
.
Wniosek
Tw:
Jeśli funkcja f jest ciągła w ![]()
, to funkcja 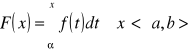
jest funkcją pierwotną funkcji f w przedziale ![]()
.
Wyszukiwarka
Podobne podstrony:
Calka oznaczona
RACHUNEK CAŁKOWY. CAŁKA OZNACZONA I JEJ ZASTOSOWANIA, SZKOŁA, Matematyka, Matematyka
calka oznaczona Wronicz id 1079 Nieznany
Calka oznaczona zadania
Zestaw 9 Całka oznaczona, pole obszaru, całka niewłaściwa
całka oznaczona
5 Całka oznaczona 3 przykładowe rozwiązania
Calka oznaczona teoria
całka oznaczona
sem2 ZJAZD 6 CALKA OZNACZONA wer 2
mat, fiz, pnom, Pole-pod-krzywa-a-calka-oznaczona[2], POLE POD KRZYWĄ A CAŁKA OZNACZONA
2 Całka oznaczona
07 energ całka oznaczona
5 4 Całka oznaczona Riemanna
1 Całka oznaczona
matma, CAŁKA OZNACZONA = liczba, CAŁKA NIEOZNACZONA = funkcja
więcej podobnych podstron