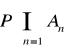
Kolokwium I z rachunku prawdopodobieństwa

8 kwietnia 1998

Imię i Nazwisko..................................................grupa.............................................

1. Z przedziału <0,2> wybieramy losowo dwa punkty x i y. Dla jakich a∈R prawdopodobieństwo zdarzenia xy ≤ a jest większe od 1/2?

2. Rzucamy jednocześnie dwiema kostkami do gry tak długo, aż suma oczek na obu kostkach wyrzuconych w jednym rzucie jest równa 7. Obliczyć:

a) prawdopodobieństwo zdarzenia, że wykonamy parzystą liczbę rzutów.

b) wartość oczekiwaną liczby rzutów.

3. Jednowymiarowa zmienna losowa X ma rozkład o funkcji gęstości

a) Obliczyć stałą c.

b) Wyznaczyć dystrybuantę zmiennej X.

b) Obliczyć EX i D²X.

c) Wyznaczyć funkcję gęstości rozkładu zmiennej .

4. Dwuwymiarowa zmienna losowa ma rozkład o funkcji gęstości

gdzie D jest trójkątem o wierzchołkach (0,0), (3,0), (3,3).

a) Wyznaczyć stała c.

b) Wyznaczyć rozkłady brzegowe.

c) Obliczyć prawdopodobieństwo zdarzenia, że .

5. Niezależne zmienne losowe X₁, X₂ mają jednakowy rozkład Bernoulliego z parametrami n  5, . Obliczyć współczynnik korelacji zmiennych Y₁, Y₂, jeśli

.

6. Niech A i B będą niezależnymi zdarzeniami losowymi takimi, że oraz . Czy zdarzenia losowe , są również niezależne?

Kolokwium I z rachunku prawdopodobieństwa

8 kwietnia 1998

Imię i Nazwisko..................................................grupa.............................................

1. Z przedziału <0,1> wybieramy losowo dwa punkty x i y. Dla jakich a∈R prawdopodobieństwo zdarzenia xy ≥ a jest większe od 1/2?

2. Rzucamy jednocześnie trzema monetami tak długo, aż otrzymamy jednakowe wyniki na trzech monetach wyrzuconych w jednym rzucie. Obliczyć:

a) prawdopodobieństwo zdarzenia, że wykonamy parzystą liczbę rzutów.

b) wartość oczekiwaną liczby rzutów.

3. Jednowymiarowa zmienna losowa X ma rozkład o funkcji gęstości

a) Obliczyć stałą c.

b) Wyznaczyć dystrybuantę zmiennej X.

b) Obliczyć EX i D²X.

c) Wyznaczyć funkcję gęstości rozkładu zmiennej .

4. Dwuwymiarowa zmienna losowa ma rozkład o funkcji gęstości

gdzie D jest trójkątem o wierzchołkach (0,0), (4,0), (4,).

a) Wyznaczyć stała c.

b) Wyznaczyć rozkłady brzegowe.

c) Obliczyć prawdopodobieństwo zdarzenia, że .

5. Niezależne zmienne losowe X₁, X₂ mają jednakowy rozkład zero-jedynkowy z parametrem . Obliczyć współczynnik korelacji zmiennych Y₁, Y₂, jeśli

.

6. Niech A i B będą niezależnymi zdarzeniami losowymi takimi, że oraz . Czy zdarzenia losowe , są również niezależne?

Kolokwium I z rachunku prawdopodobieństwa

17 listopada 1999

Imię i Nazwisko.........................................................................nr indeksu...................

Nr grupy...............

1. Z obszaru wybieramy losowo punkt (x,y). Obliczyć prawdopodobieństwo zdarzenia, że .

2. Z talii 52 kart losujemy jedną kartę (po każdym losowaniu wkładamy wylosowane kartę z powrotem do talii) tak długo, aż wylosujemy kiera. Obliczyć prawdopodobieństwo zdarzenia, że liczba wykonanych doświadczeń będzie podzielna przez 3.

3. Zmienna losowa X ma rozkład o funkcji gęstości

a) Wyznaczyć stałą c.

b) Obliczyć EX i .

c) Wyznaczyć funkcję gęstości rozkładu zmiennej .

4. Rzucamy dwa razy kostką do gry. Niech będzie zmienną określoną wzorem

a − zmienną określoną wzorem

a) Wyznaczyć rozkład dwuwymiarowej zmiennej losowej .

b) Wyznaczyć dystrybuantę zmiennej .

5. Dane są takie trzy łącznie niezależne zdarzenia losowe , że dla i = 1,2,3.

a) Obliczyć .

b) Obliczyć .

Kolokwium I z rachunku prawdopodobieństwa

17 listopada 1999

Imię i Nazwisko.........................................................................nr indeksu...................

Nr grupy...............

1. Z obszaru wybieramy losowo punkt (x,y). Obliczyć prawdopodobieństwo zdarzenia, że .

2. Rzucamy dwiema kostkami do gry tak długo, aż suma oczek na obu kostkach wyrzuconych w jednym rzucie będzie równa 7. Obliczyć prawdopodobieństwo zdarzenia, że liczba wykonanych doświadczeń będzie podzielna przez 4.

3. Zmienna losowa X ma rozkład o funkcji gęstości

a) Wyznaczyć stałą c.

b) Obliczyć EX i .

c) Wyznaczyć funkcję gęstości rozkładu zmiennej .

4. Rzucamy trzy razy monetą. Niech będzie zmienną określoną wzorem

a − zmienną określoną wzorem

a) Wyznaczyć rozkład dwuwymiarowej zmiennej losowej .

b) Wyznaczyć dystrybuantę zmiennej .

5. Dane są takie trzy łącznie niezależne zdarzenia losowe A, B, C, że ,

, .

a) Obliczyć .

b) Obliczyć .

Kolokwium I z rachunku prawdopodobieństwa

7 kwietnia 1999

Imię i Nazwisko...................................................................nr indeksu......................

1. Z przedziału <0,1> wybieramy losowo dwie liczby x i y. W zależności od wartości parametru a ∈ R wyznaczyć prawdopodobieństwo zdarzenia, że .

2. W książce mającej 120 stron znajduje się 48 błędów. Obliczyć przybliżoną wartość prawdopodobieństwa, że na 50 stronie znajdują się co najmniej 2 błędy.

3. Zmienna losowa X ma rozkład bezwzględnie ciągły o funkcji gęstości określonej wzorem

a) Wyznaczyć stałą c.

b) Obliczyć EX i D²X.

4. Niezależne zmienne losowe mają jednakowy rozkład Pareto o funkcji gęstości

a) Wyznaczyć stałą c.

b) Wyznaczyć funkcję gęstości rozkładu prawdopodobieństwa zmiennej , gdzie , .

5. Wykazać, że dla dowolnego wstępującego ciągu zdarzeń losowych spełniony jest warunek .

Kolokwium I z rachunku prawdopodobieństwa

7 kwietnia 1999

Imię i Nazwisko...................................................................nr indeksu......................

1. Z przedziału <0,1> wybieramy losowo dwie liczby x i y. W zależności od wartości parametru a ∈ R wyznaczyć prawdopodobieństwo zdarzenia, że .

2. W książce mającej 150 stron znajduje się 45 błędów. Obliczyć przybliżoną wartość prawdopodobieństwa, że na 48 stronie znajdują się co najwyżej 3 błędy.

3. Zmienna losowa X ma rozkład bezwzględnie ciągły o funkcji gęstości określonej wzorem

a) Wyznaczyć stałą c.

b) Obliczyć EX i D²X.

4. Niezależne zmienne losowe mają jednakowy rozkład Pareto o funkcji gęstości

a) Wyznaczyć stałą c.

b) Wyznaczyć funkcję gęstości rozkładu prawdopodobieństwa zmiennej , gdzie , .

5. Niech będzie zstępującym ciągiem zdarzeń takim, że. Wykazać, że.

Kolokwium I z rachunku prawdopodobieństwa

Imię i Nazwisko.......................................................................................................

1. Z przedziału <2,1> wybrano losowo dwie liczby x i y. W zależności od wartości parametru a∈R obliczyć prawdopodobieństwo zdarzenia, że x  y ≤ a.

2. Doświadczenie polegające na rzucie trzema monetami powtarzamy tak długo, aż wyrzucimy trzy orły.

a) Obliczyć prawdopodobieństwo zdarzenia, że liczba doświadczeń będzie podzielna przez trzy.

b) Obliczyć wartość oczekiwaną liczby doświadczeń.

Wsk. dla |x|  1.

3. Zmienna losowa X ma rozkład o funkcji gęstości

a) Wyznaczyć stałą c.

b) Wyznaczyć dystrybuantę zmiennej X.

c) Wyznaczyć rozkład zmiennej .

4. Dwuwymiarowa zmienna losowa ma rozkład o funkcji gęstości

gdzie

a) Wyznaczyć stałą c.

b) Wyznaczyć rozkłady brzegowe zmiennych .

c) Zbadać niezależność zmiennych .

5. Obliczyć współczynnik korelacji , jeśli zmienna ma rozkład o stałej gęstości w trójkącie o wierzchołkach (0,0), (0,1), (1,1).

Kolokwium I z rachunku prawdopodobieństwa

Imię i Nazwisko.......................................................................................................

1. Z przedziału <1,2> wybrano losowo dwie liczby x i y. W zależności od wartości parametru a∈R obliczyć prawdopodobieństwo zdarzenia, że x  y ≤ a.

2. Doświadczenie polegające na rzucie dwiema kostkami powtarzamy tak długo, aż wyrzucimy dwie szóstki.

a) Obliczyć prawdopodobieństwo zdarzenia, że liczba doświadczeń będzie podzielna przez cztery.

b) Obliczyć wartość oczekiwaną liczby doświadczeń.

Wsk. dla |x|  1.

3. Zmienna losowa X ma rozkład o funkcji gęstości

a) Wyznaczyć stałą c.

b) Wyznaczyć dystrybuantę zmiennej X.

c) Wyznaczyć rozkład zmiennej .

4. Dwuwymiarowa zmienna losowa ma rozkład o funkcji gęstości

gdzie

a) Wyznaczyć stałą c.

b) Wyznaczyć rozkłady brzegowe zmiennych .

c) Zbadać niezależność zmiennych .

5. Obliczyć współczynnik korelacji , jeśli zmienna ma rozkład o stałej gęstości w trójkącie o wierzchołkach (0,0), (1,0), (1,1).

Kolokwium I z rachunku prawdopdobieństwa

Imię i Nazwisko..................................................................................................

1. Wybieramy losowo dwie liczby a i b z przedziału <-2,2>. Obliczyć prawdopodobieństwo zdarzenia, że .

2. Ze zbioru liczb 1,2,...,300 losujemy 10000 razy ze zwracaniem po jednej liczbie. Wyznaczyć przybliżoną wartość prawdopodobieństwa zdarzenia, że otrzymamy nie więcej liczb parzystych niż nieparzystych.

3. Zmienna losowa X ma rozkład o funkcji gęstości

a) Wyznaczyć stałą c.

b) Obliczyć EX i D²X.

c) Wyznaczyć rozkład zmiennej Y = X².

d) Obliczyć EY.

4. Rzucamy dwukrotnie kostką sześcienną. Niech zmienna X₁ oznacza wartość bezwzględną różnicy liczb wyrzuconych oczek, a X₂ będzie zmienną taką, że

a) Wyznaczyć rozkład dwuwymiarowej zmiennej losowej .

b) Wyznaczyć rozkłady brzegowe.

c) Zbadać niezależność zmiennych X₁ i X_2.

5. Dany jest ciąg zdarzeń losowych takich, że i dla n∈N. Obliczyć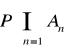
.

---