61414

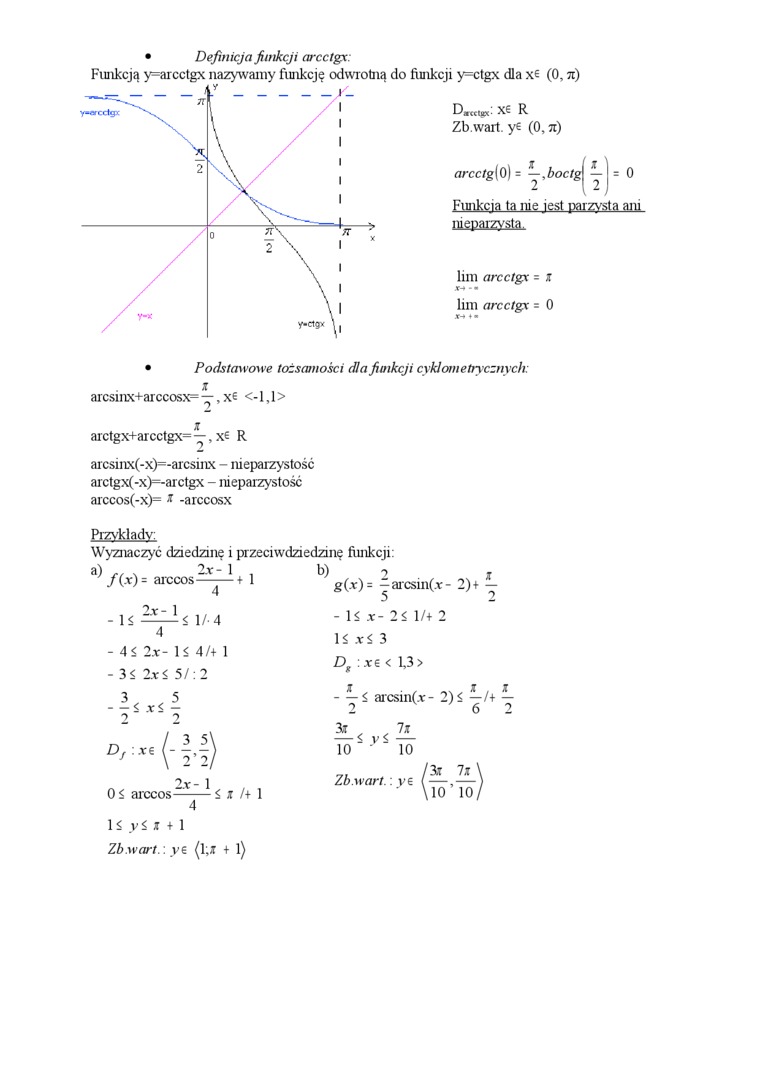
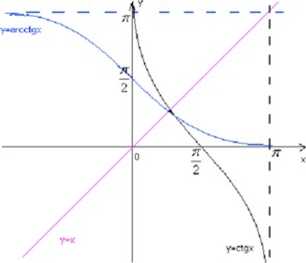
• Definicja fitnkcji arcctgx:

Funkcją y=arcctgx nazywamy funkcję odwrotną do funkcji y=ctgx dla x£ (0, tc)

xe R

Zb.wart. y€ (0, n) arcctg{0) = y ,6oc/gj y j = 0 Funkcja tą nie jest parzysta ai\i

nieparzysta.

lim arcctgx = x

x-» -•

lim arcctgy - 0

.«-»♦«

• Podstawowe tożsamości dla funkcji cyklonietrycznych:

X

arcsinx+arccosx= —, x€ <-1,1 > x

arctgx+arcctgx= —, x£ R

arcsinx(-x)=-aicsinx - nieparzystość arctgx(-x)=-arctgx - nieparzystość arccos(-x)= ¹ -arccosx

Przykłady:

Wyznaczyć dziedzinę i przeciwdziedzinę funkcji a) .    2x- 1    b)    o

4

2x- 1

- 1<    1/4

4

-    4< 2x- 1< 4/+ 1

-    3< 2x< 5/: 2

3    5

-    < x < —

2    2

^D'^xi (-!•!)

2r- 1

Oś arccos-< x /+ 1

g(.v)= y arcsin(x - 2)+ -

-    1< *- 2 < 1/ł 2

lś xś 3 :xe < 1,3 >

-    y ś aicsin(.r- 2)ś y/+

o

3ł ,    7i

10 '    10

Zb.wart.: ve

/3x_ 7x_\ \ 10 ’ 10 /

1

< v < x + 1 Zb.wart.: ve (l;i + l)