38509

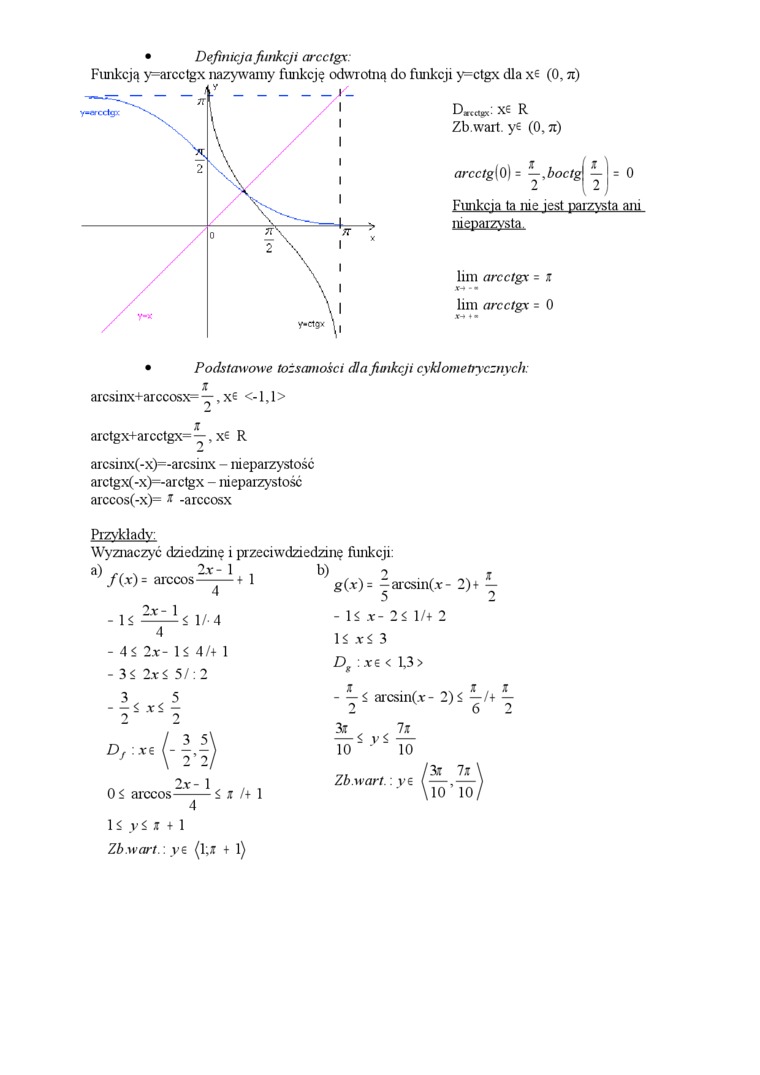
•    Definicja funkcji arcctgy:

Funkcją y=arcctgx nazywamy funkcję odwrotną do funkcji y=ctgx dla xe (0, n)

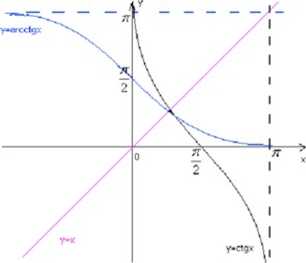
D««t«x R Zb.wart. y€ (0, n)

arcctg{0) = y-,6oc/gj y = 0 Fiutkcją tą nję jest paizy>ta ai\i

nieparzysta, lim arcctgx = x

x-» -•

lim arcctgy - 0

.«-»♦«

• Podstawowe tożsamości dla funkcji cyklometrycznych:

X

arcsinx+arccosx= —, x€ <-1,1 >

*7

X

arctgx+arcctgx= —, x£ R

arcsinx(-x)=-aicsinx - nieparzystość arctgx(-x)=-arctgx - nieparzystość arccos(-x)= ¹ -arccosx

Przykłady:

Wyznaczyć dziedzme i przeciwdziedzine fiuikcji:

o

a) ,₍ .    2x- 1

f(x) = arccos-+ 1

4

2x- 1

- 1<    1/4

4

-    4< 2x- 1< 4/+ 1

-    3< 2x< 5/: 2

o    x

g(x)= j arcsin(.v - 2) + -

- 1< *- 2 < 1/+ 2 H 3 : xe < 1,3 >

- y-ś aicsin(.y- 2)ś ^-/t

D₇ : xe

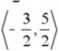
2.v- 1 4

7x

— ś v < — 10 ’ 10

0 < aiccos

$ x /+

1

Zb.wart.: ve

1

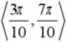
< y < I + 1 Zb.wart.: ve (l;i + l)