048

Równania i nierówności

wymierne

DEFINICJE

W(x)

Funkcją wymierną nazywamy funkcję F(x) = ~pyy gdz.ie W(x) i P(x) są wielomianami i P(x) ^ 0. Dziedziną tej funkcji jest zbiór D_F = R\ {.v: P(x) = 0}. RÓWNANIA WYMIERNE - przykładowe zadania

DEFINICJA

Równaniem wymiernym nazywamy równanie postaci

W(x)

P(x)

= 0,

gdzie fV(x) i P(x) oznaczają wielomiany oraz P(x) ^ 0.

Przy rozwiązywaniu tego typu równań pamiętaj o dziedzinie!

ZADANIE 1

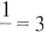
x

Założenia:

A' 0, czyli D = R \ J 0}    Dlatego, ie mianownik nie może być równy zero,

Rozwiązanie:

- = 3 /• x x

Mnożymy obie strony równania przez x, by uwolnić się od ułamka.

95