002

Oto definicja całki oznaczonej funkcji f(x) w przedziale [a, 6],

Dla każdej z liczb n = 2,3,... czynimy co następuje. Przedział [.a, 6] dzielimy na przedziały punktami ... , £_n_i takimi, że a =    < X\ < * ■ ♦ < x_n_i < x_n = 6. Długości kolej-,

nych przedziałów    [#1,^2], ,    , [a:_n-i,3:_n] oznaczamy przez Ai,A2« . ,A_n. Naj

większą z tych liczb nazywamy normę podziału* Bierzemy pewne liczby ai £ [x_0fxi], £

. , u_n £    .r_n]- Tworzymy następującą sumę, zwaną sumę całkową-.

n

a_n= A_i/(u₁) + A₂/(w₂)+    + A„/(«„) (czyli y^A_fc/(«_fc) ).

k=l

Jeżeli f(x) > 0 w przedziale [a, 6], to sensem geometrycznym sumy całkowej jest pole tzw. figury schodkowej (zacieniowanej na rysunkach). Oto rysunki dla n = 2, n = 3, n = 4 oraz dla dowolnego n:

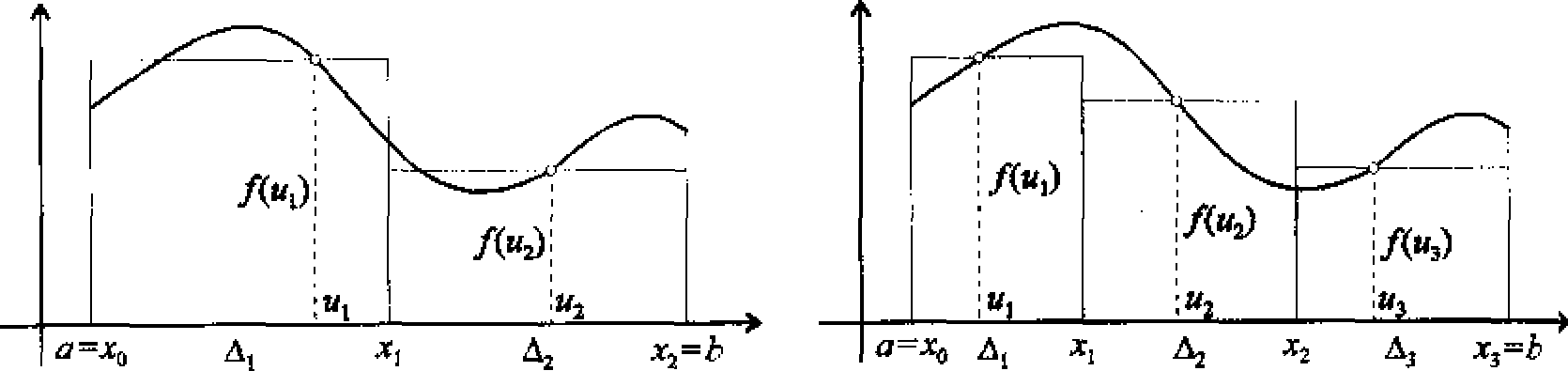
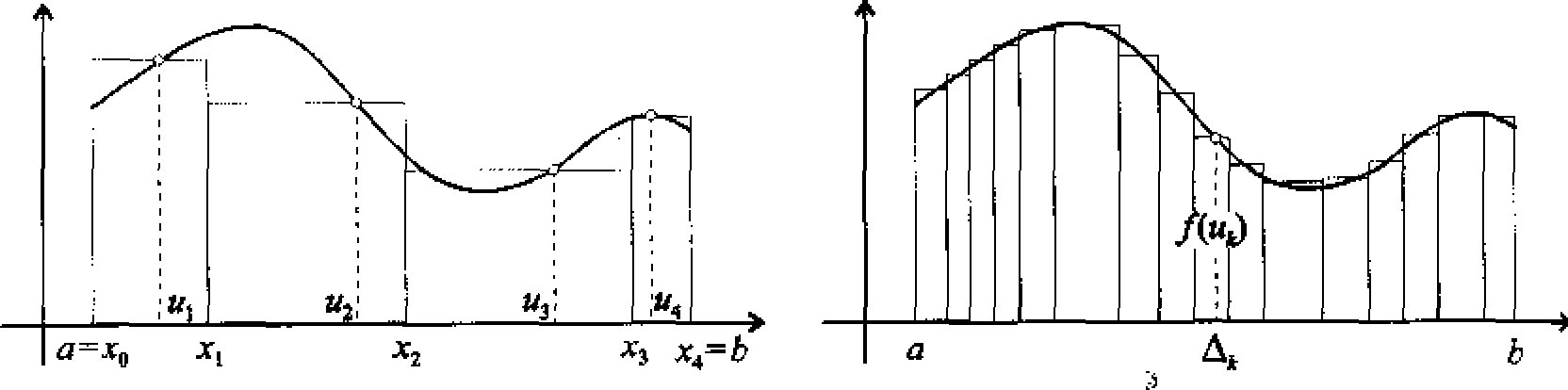
O ile istnieje i jest skończona granica ciągu sum całkowych cr_n przy n —► 00 i gdy zachodzą poniższe założenia 1-3, to granicę tę nazywamy całką oznaczoną funkcji f(x) w przedziale

b

[a, b]. Oznaczamy ją symbolem / f(x) dx< Oto założenia 1-3:

a

1.    Norma podziału musi zmierzać do 0, gdy n zmierza do 00.

2.    Granica nie może zależeć od wyboru punktów x\. ... , x_n„i dla n = 2,3,

3.    Granica nie może zależeć od wyboru punków u\, .., ,u_n dla n ~ 2,3, ....

Krótko: lim o_n = J f(x) dx, jeżeli granica ta jest skończona i zachodzą założenia 1-3.

Trapezem krzywoliniowym nazywamy figurę ograniczoną osią Ox, wykresem krzywej y = f(x) i dworna pionowymi odcinkami o końcach (a, 0), (a, f(a)) oraz (b, 0), (b,f(b)).

Z definicji całki oznaczonej wynika, że jej sensem geometrycznym (gdy f(x) > 0 w [a, 6]) jest pole trapezu krzywoliniowego* Ilustrację tego widzimy na powyższych rysunkach a

86