82497

Część 2 4. RAMY OBCIĄŻONE TERMICZNIE. OSIADANIEM PODPÓR ORAZ PRZYPADKI... 22

Zajmijmy się najpierw składnikiem równania obliczonym dla podpory niepodatnej. Skorzystamy pizy tym ze znanych nam wzorów transformacyjnych, przyjmując, że tylko podpora / doznaje obrotu (<p,=J .

w ^3EJ i    \ ^3EJ

M_ń=—j—[<p-V_ś)=—j-

(4.50)

Następnie obliczmy wartość momentu, który powstame w wyniku podparcia sprężystego, gdzie kąt obrotu cięciwy pręta «/>,* wynosi:

(4.51)

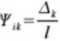
(4.52)

to pizenueszczenie końca belki, które powstanie z uwagi na podparcie w punkcie k podporą sprężystą o sztywności k .

^A‘=^R‘i

(4.53)

Podstawiając wartości (4.52) i (4.53) do równania (4.51) otizymujemy:

• JEJ ,    , JEJ 4. JEJ E,

(454)

Zapisując iównaiue siuny momentów' względem punktu / otrzymujemy w^ość reakcji w podporze k:

!«,=«

R,= ^Y    (4.55)

Po podstawieniu równania (4.55) do (4.54) otizymujemy:

A/" =

3 EJ M_lt l^:    /

l

K

3 EJ

' r

M,

l

K

Wprowadzając podstawieiue:

kI^s EJ

otizymujemy:

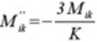
(456)

AlmaMater

Dobra D.. Dztakicwlcz L, Jambrożrk S.. Kotnona M.. Mikołajczak K.. Przybylaka P., Sytak A.. Wdowdca A