84725

W fazie wzrostu logarytmicznego wzrost podlega zasadom kinetyki I rzędu względem stężenia biomasy. Równanie (1) sprowadza się do postaci (2), gdzie właściwa szybkość wzrostu jest odpowiednikiem stałej szybkości reakcji.

^ = H X    (2)

dt

Po scałkowaniu równania (2) dla zakresu odpowiadającego wzrostowi logarytmicznemu uzyskuje się zależność:

ln X,-ln X,=p •(/,-/,)    (3)

gdzie: X_u X₂- graniczne stężenie biomasy w obrębie wzrostu logarytmicznego (g l'^ll ti, t₂- czasy odpowiadające odpowiednio X₂, X₂ [h]

Wartość właściwej szybkości wzrostu jest zależna od szczepu mikroorganizmów, warunków fizycznych (T, pH, siła jonowa) oraz jest funkcją stężenia substratu (ów) (zwykle substratu węglowego stanowiącego główne źródło węgla i energii, nazywane substratem limitującym). Najprostszym, ale najczęściej spotykanym modelem opisującym relację właściwej szybkości wzrostu i stężenia substratu limitującego jest model przedstawiony przez Monoda:

(4)

K_s+c_s

gdzie: <*-stężenie substratu limitującego(g I¹]

K_s-stała Monoda [g I'¹]

(irrun maksymalna szybkość wzrostu (h'^x)

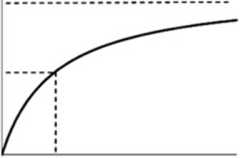
Zależność ta, analogiczna do równania Michaelisa-Menten, przedstawiona jest schematycznie na Rys. 2.

A

Ks    Cj

Rys. 2 Zależność właściwej szybkości wzrostu od stężenia substratu limitującego opisana modelem Monoda.

Stałe powyższego równania kinetycznego można wyznaczyć zarówno przy wykorzystaniu wyników z hodowli okresowej, jak i z hodowli ciągłej. Realizacja hodowli ciągłej jest znacznie bardziej skomplikowana, aniżeli hodowli okresowej, stąd przynajmniej wstępne wartości stałych wyznacza się na podstawie danych z hodowli okresowej.