95672

Zadania z algebry dwudniowej (zestaw 2)

Geometria przestrzeni Euklidesowych

Wykorzystując iloczyn skalamy udowodnić następujące twierdzenia dotyczące przestrzeni euklidesowej:

1.    Wysokości dowolnego trójkąta przecinają się w jednym punkcie.

2.    Sy metraInc boków dowolnego trójkąta przecinają się w jednym punkcie.

3.    W dowolnym trójkącie punkty przecięcia się środkowych, wysokości i symetralnych boków leżą na jednej prostej.

4.    Twierdzenie cosinusów. Jeżeli A.B.Csą trzema różnymi punktami przestrzeni euklidesowej. to

|| AB ||²= || BC ||² + || CA ||² -2 || CA || • || BC || .cos(Z{Ot,ĆB}).

Wyprowadź stąd twierdzenie Pitagorasa.

5.    Jeżeli A.B.C są trzema różnymi punktami przestrzeni euklidesowej. to

(FA.CB) = 11^'II¹ + II tB II²-li AB II² _

6.    Jeżeli A.B.C są wierzchołkami trójkąta oraz punkt /żjest rzutem punktu C na prostą AB (s/nnlek wysokości trójkąta ABC), to || CD ||²= (C4.CB) - (DA.DB).

Ponadto jeśli wektory CA, CB są prostopadle, to || CD ||²= || DA || • || DB ||.

7.    Jeżeli A.B.C są wierzchołkami trójkąta oraz punkt Sjest środkiem odcinka AB, to

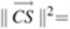
2 II CA II² +2 || CB ||² - || AB ||² 2

II CS ||²=|| CA II ■ II CB II -cos(Z{CA,CB})+ II AB ||² oraz

8. Twierdzenie sinusów. Jeżeli A.B.C są wierzchołkami trójkąta, to

l|A£ll_ ₌ l|g£ll_ ₌    \\AB\\_

sin(Z{ft4.flC}) sin(Z{Afl,AC}) sin(Z{CA.Cfl})

9. Wzór Merona. Pole trójkąta o bokach a.b.c wyraża się wzorem s \/p(p a){p b)(p -<•), gdzie p    .

10. Twierdzenie Ptolemeusza. W czworokącie wpisanym w okrąg iloczyn długości przekątnych jest równy sumie iloczynów długości boków przeciwległych.

Wskazówki do rozwiązania powyiszych zadań a takie dowody wielu innych interesujących faktów geometrycznych moim zmletć w ksiąice Edwarda Piekuta pi.., Wektory i geometria". PZWS. Warszawa 1964.

2