2100419939

a) Funkcja / jest ciągła w każdym punkcie x / 2 jako iloraz funkcji ciągłych. Osobnego sprawdzenia wymaga ciągłość w punkcie x = 2. Warunek ciągłości w tym punkcie jest następujący: lim f(x) = /(2).

Obliczamy więc:

lim f(x) = lim

x-»2    ' ⁷

2 x - 2

(x~2)(x + 2)

= lim(x + 2) = 4.

i-2

Z drugiej strony, /(2) = 4. więc warunek ciągłości w punkcie x = 2 jest

spełniony. Podsumowując, funkcja / jest ciągła w każdym punkcie swojej dziedziny - taką funkcję nazywamy ciągłą.

b) Aby znaleźć granicę funkcji / w punkcie x = 1 obliczamy granice jednostronne w tym punkcie: lim /(i) = lim (3x² — x — 1) = 1,

X-»l^_    X-*l“

lim f(x) = lim (5x — 3) = 2.

x-»l+    *-»i⁺

Granice te nie są sobie równe, więc granica funkcji / w punkcie x = 1 nie istnieje. Funkcja / nie jest więc ciągła w tym punkcie.

a)    /(*) =

b)    /(i) =

Zadanie 5. Znaleźć równania asymptot funkcji 2x² + 3x + 2

x² + 4 3x² + x

x — 1 Rozwiązanie.

a) Dziedziną funkcji / jest zbiór wszystkich liczb rzeczywistych, więc wykres funkcji nie posiada asymptoty pionowej. Aby otrzymać asymptotę poziomą obliczamy granicę funkcji w nieskończoności:

lim

x—oc

2 x² + 3x + 2 x² -t- 4

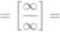
lim

x-*±oo

*²(l + £)

10

= 2