426907384

Wykład 1

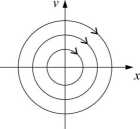
Rysunek 1.6: Oscylator harmoniczny

Rozważmy funkcję E(x,v) ⁼ \ ^Jr\- Zauważmy, że otrzymany układ równań można zapisać w postaci

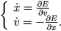
Tego typu układy nazywamy układami Hamiltonowskimi. Funkcja E jest stała na trajektoriach układu. Można się o tym przekonać różniczkując funkcję E(x(t), v(t)):

dE_dE_ . dE_ . _dE_dE__dE_dE_

dt dx ^{X +} dv ^V dx dv dv dx

Funkcję E nazywamy energią, składnik ^ - energią potencjalną, zaś y - energią kinetyczną.