68836 img458

2.3. Funkcja pochodna

Rozważmy funkcję f(x) = 'ix. Wiemy, że D_f = (O, +oo). Wykorzystując znane nam już wiadomości, możemy obliczyć wartość pochodnej tej funkcji w pew-

itd. Z przykładu 3. wiemy, że nie istnieje /'+(0). Zatem możemy obliczyć /’(x₀) dla dowolnego

x₀ e (0, +oo). Mamy:    o

t

nych punktach, np.: /'(4) = ^ , /'(9) = 1, /'

lim

h->0

h

0    h

(x₀+h) - (x₀)    _

^/ł->0 h (ylx₀+h + Vxó)

= lim

^h^° (^lx₀+h + Vxb)

Otrzymaliśmy więc f(x₀) = —dla x₀ e (0, +oo).

2 vx₀

Wykorzystując powyższe obliczenia, możemy teraz utworzyć nową funkcję, która każdej liczbie rzeczywistej x (w tym wypadku dodatniej) przyporządkuje liczbę równą /'(x).

W naszym przypadku liczbie x = 4 przyporządkujemy liczbę -, liczbie x = -

-^2    i

przyporządkujemy liczbę —. Ogólnie liczbie x = x₀ przyporządkujemy liczbę —'-j=.

2    2Vx₀

Oczywiście argumentami tej nowej funkcji nie mogą być ani liczby ujemne (nie należą one bowiem do dziedziny naszej funkcji i wobec tego dla nich nie możemy utworzyć ilorazu różnicowego), ani liczba 0 (nie istnieje bowiem /'+(0)). Ta nowa funkcja jest oczywiście związana z funkcją /, dlatego przyjęto zasadę, by oznaczać ją /' i nazywać funkcją pochodną funkcji / lub krótko: pochodną funkcji /.

Możemy teraz zapisać wzór tej funkcji:

1

r w =

xe (0, +oo).

2V7’

WNIOSEK

Jeżeli/W=V7, xe(0, +oo),

to/'(*) =

2VT

xe (0, +oo).

Czasami treść tego wniosku bywa zapisywana krócej 1

X -

27T

xe (0, +oo).

Uwaga:

Z.iuważ, że w tym wypadku D_r* D,, czyli dziedzina danej funkcji i dziedzina jej pochodnej nie muszą być równe. Zawsze natomiast musi być spełniona zależność D_rczDf.

Przejdźmy teraz do zdefiniowania pochodnej dowolnej funkcji.

DEFINICJA 6.

Niech / będzie dowolną funkcją określoną w zbiorze D_f. Funkcję, która każdej liczbie x₀ g D_f przyporządkowuje liczbę /'(x₀) (o ile istnieje /' (x₀)) nazywamy funkcją pochodną funkcji / lub pochodną funkcji / i oznaczamy /'. Zbiór tych x₀ g D_f, dla których istnieje /'(x₀) stanowi dziedzinę funkcji /' i będziemy go oznaczać D_r.

Pochodną funkcji oznacza się również:

d/(x)

dx

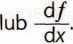
Uwaga

Nie należy mylić terminów: pochodna funkcji w punkcie i pochodna funkcji (funkcja pochodna). Pochodna funkcji w punkcie x₀ jest to granica odpowiedniego ilorazu różnicowego (jeśli istnieje), a więc jest to liczba. Natomiast pochodna funkcji jest to funkcja, która argumentowi x₀ przyporządkowuje liczbę równą pochodnej funkcji w punkcie x₀.

PRZYKtAD 5.

Wyznaczmy pochodne funkcji:

a)    f(x) =c,cefi;

b)    f{x) = ox + b, a, b e R;

c)    f(x) = xⁿ, n g N₊.

Ad a) Zauważmy, że D_f - R. Weźmy dowolne x₀ e R. Mamy:

.. /(x₀+h) -/(x₀)    .. c-c    .

|j_m    o—i—Ł±OL - ||_m -= o,

fi—>0    h-> O ff

gdyż w ułamku występującym w ostatniej granicy licznik jest równy zeru, a mianownik jest różny od zera, zatem cały ułamek jest równy zeru, a więc granica ta jest też równa zeru.

Otrzymujemy stąd /' (x) = O i D_f< - R.