7090997021

przy założeniu, że więzy „m” nie pokrywają się z więzami „k”. Ponieważ mechanizm przedstawia sobą łańcuch kinematyczny, to do określenia jego ruchliwości stosujemy te same wzory strukturalne.

3.1.2. Klasyfikacja płaskich mechanizmów

Ogólnie przyjęto klasyfikację opracowaną przez Assura-Artobolewskiego, która opiera się na pojęciu grupy i 4 założeniach.

Grupą Assura nazywamy otwarty łańcuch kinematyczny, który dołączony do ostoi posiada ruchliwość zerową.

Przyjęte założenia:

1.    Liczba członów napędzających równa jest ruchliwości mechanizmu.

2.    Człony napędzające wchodzą w pary kinematyczne z ostoją.

3.    Wszystkie pary kinematyczne rozpatrywanego mechanizmu są V klasy.

4.    Człon napędzający wraz z ostoją tworzy grupę I klasy.

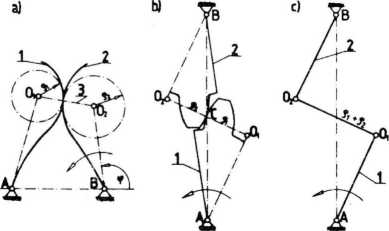
Jeśli w mechanizmie jest para IV klasy, np. krzywkowa (rys. 3.la), lub para zazębienia (rys. 2.Ib), to zastępujemy ją łańcuchem kinematycznym przez dołączenie 1 członu i 2 par Ol, 02 V klasy (rys. 3.1a,c).

Rys. 3.1. Sposób zastąpienia pary kinematycznej czwartej klasy, łańcuchem kinematycznym z parami V klasy.

Zgodnie z tą klasyfikacją złożone mechanizmy otrzymujemy w wyniku dołączenia do członu napędzającego grup Assura. Grupy Assura dzielą się na klasy, a wewnątrz każdej klasy na rzędy, zaś wewnątrz rzędów na postacie, odmiany i modyfikacje.

Klasę grupy Assura definiujemy powiększonym o jeden najwyższym wymiarem sympleksu euklidesowego, który w niej można wyodrębnić.

Sympleks posiada wymiar r, jeśli jest utworzony z r+1 wierzchołków, które w grupach Assura odpowiadają parom kinematycznym. Jeśli przyjąć umownie liczbę wierzchołków sympleksu za wymiar konturu, to klasę grupy można również zdefiniować wymiarem konturu. W tabl. 3.3 pokazano sympleksy: jednowymiarowy - człon, dwuwymiarowy - trójkąt złożony z 3 członów, trójwymiarowy - czworobok złożony z 4 członów, czterowymiarowy - pięciobok złożony z 5 członów.

20