8416073540

opracowane w tym celu metody obliczeniowe. Jedną z nich jest, poznana już przez nas w wersji dla obwodów prądu stałego, metoda przekształcania obwodu. Nazywana ona bywa też metodą zwijania a także metodą elementów zastępczych (albo gałęzi zastępczych). Jej charakterystyczną cechąjest to, że bezpośrednio, już w trakcie obliczeń, daje użyteczne wyniki cząstkowe.

Metoda zwijania polega na zastępowaniu - do celów obliczeniowych - poszczególnych części obwodu układami równoważnymi, najczęściej gałęziami równoważnymi (nazywanymi też gałęziami zastępczymi). Równoważność polega tu na tym, że parametry układu równoważnego (gałęzi równoważnej) są tak dobrane, aby po zastąpieniu nim (nią) danej części obwodu, rozpływ prądów i rozkład napięć w pozostałej części obwodu nie uległ zmianie.

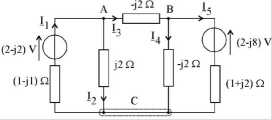
Rys. 9.3a. Schemat zastępczy obwodu przykładowego I po pierwszym etapie przekształcania

Reguły tworzenia gałęzi zastępczych dla szeregowych i równoległych połączeń gałęzi pasywnych i aktywnych są analogiczne do reguł znanych nam z teorii obwodów prądu stałego (por. pkt 2.4. rozdz. 2. pierwszej części niniejszego skryptu). Różnica polega na tym, że zamiast rezystancji występują impedancje zespolone (niektóre z nich mogą być rezystancjami), a zamiast sił elektromotorycznych    i

prądomotorycznych ich wartości skuteczne zespolone.

Zastosujmy    metodę

przekształcania obwodu do wyznaczania prądów płynących w obwodzie przykładowym I. Jego schemat zastępczy został przedstawiony na rys. 9.1., a schemat zastępczy z danymi do stosowania metody symbolicznej na rys. 9.2.

Przekształcanie obwodu zaczniemy od zwinięcia elementów połączonych szeregowo. W poszczególnych gałęziach dodajemy do siebie impedancje zespolone połączonych szeregowo elementów pasywnych i wartości skuteczne zespolone połączonych szeregowo sił elektromotorycznych:

Zj=i+ji+(-J2)=(1-ji)n, Z_z5=i+j2=(i+J2)n

E₅ =2-j8 = (2-j8)V

W efekcie otrzymujemy schemat, w którym w gałęziach występują albo pojedyncze impedancje zespolone, albo idealne źródła napięciowe połączone szeregowo z impedancjami zespolonymi. Schemat ten pokazano na rys 9.3a. Ponieważ symbolami elementów pasywnych są tutaj prostokąciki (a nie symbole odpowiednich elementów idealnych), więc wartości skuteczne zespolone muszą być zapisane jako liczby zespolone.

Teraz możemy zwijać gałęzie połączone ze sobą równolegle.

Impedancja gałęzi zastępczej dla równoległego połączenia gałęzi „1-2” ma wartość:

(l-jl)-j2    2 + J2 2^2-e *

1- jl + j2    1 + jl

l42-t

Wartość skuteczna zespolona SEM gałęzi zastępczej dla równoległego połączenia gałęzi „1-2” wynosi:

E (2-j2)-j2_=i±j4^y

l~jl + j2    I + jl

Impedancja zespolona gałęzi zastępczej dla równoległego połączenia gałęzi „4-5”:

_z a+i2H-j2>

~⁴⁵    1 + J2- j2    ^J

-56-