9414912712

Zadania z Mechaniki - ćwiczenia audyloryjne

Z równania (4) wynika: natomiast z równania (5):

R_b = -R_Cx = 1,7 [kN] r_d = -R_Cy + P = 3,7 [kN]

Sposób II.

Zapisujemy równania równowagi dla całej ramy:

1) J^P_ix = R_Ax + Pcosa - R_B = 0

2)    -Pś\na-P-P + R_d = 0

Równanie momentów zapiszemy względem punktu A :

3) Y.M,_w = -Pa-Vr-P(2r)+R_D(2r) = 0,

gdzie:

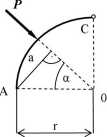
a = r sin cc —    /■ , stąd

3) IX,, =-P^r-Pr-/>(2_r)+fl_D(2r) = 0,

oraz równania równowagi dla jednej z części - prawej:

4) 2X=-/i_n-.K_JJ=⁰ S)Z^Plr=^RCy~P ⁺ R„=° fi) 2X«=-V⁺^=°

Z równania (3) wyliczamy:

-18-