9414912722

Zadania z Mechaniki - ćwiczenia audytoryjne

otrzymujemy:

IX,i = M_A -Fsina(/sinar) + Fcosa(/ + /cosa)= 0

Stąd

M_a = F/sin² a + FI cos² a + FI cos a = F/(l + cosor).

Dla kąta a = 60° otrzymujemy:

R_Ax = V3 [&V], R_Ay = 1 [/c7V], M_a =3[itAT/w]

Dla kąta a = 0 (pręt prostoliniowy):

R_Ax = 0, R_Ay = 2 [ArF], M_a = 4 [kNm]

Dla kąta a = 90° (pręt zgięty pod kątem prostym):

R_Ax = 2 [M], R_Ay = 0, M_a = 2 [kNm]

Przykład 5.

Belkę o długości 4/ zamocowaną na podporach przegubowych stałej i przesuwnej obciążono momentem M, siłą skupioną P i obciążeniem nałożonym o stałym natężeniu <y, jak pokazano na rysunku. Obliczyć wartości reakcji, jeżeli M =3[kNm], q = 1 [kN/m], P = 2 [£7V], a = 7rl6[rad] ,1 = 1 [m].

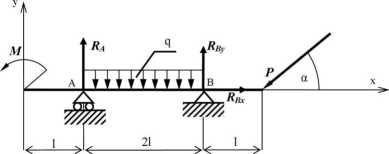
Rozwiązanie.

Układ współrzędnych zaczepimy na lewym swobodnym końcu belki. Równania równowagi płaskiego dowolnego układu sił działających na belkę mają postać:

=^Bv-^cosa = °

-9-