1053228421

— 324 -

(„la somme des nombres a et p”), en supposant que les expressions „0” („zero”) et „m/n {ę (4)}” (»le plus petit nombre

ordinal i ayant la propriete donnee”) aient ete definiesau prealable:

Y = a lorsque a, p et 7 sont des nombres ordinaux et lors-qu’il existe une fonction / satisfaisant aux conditions: (a) /(0)= a; (b) si Y]<p ou 7j = p, /(rj) est le plus petit nombre ordinal 4 tel que pour tout £ C */] on a: /(£)<£; (c) /(p) = 7.

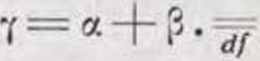
ord (a). ord (p).ord (7): •: • [3 /]    /(O) = a [rj] :

rj<p. V • 1 = PO./(rj)= min{[C] : C<**] -Z). /(4)<4} /(p) = 7

II ne faut pas croire que la definition qui precede soit un schema de toutes les definitions possibles qui s’emploient pour remplacer celles par recurrence. Certaines differences peuvent se manifester dans des details: il est necessaire parfois de distinguer p. ex. dans 1’enonce de la condition (b) deux cas suivant que rj est par hypothese un nombre de 1-ere ou de 2-de espece. Toutefois ces differences ne sont pas essentielles.

A la base du systeme d’axiomes qui precede, M. Tarski developpa ensuite les chapitres principaux de rArithmetique, montrant ainsi d’une faęon explicite, par voie — pour ainsi dire — empirique, que le systeme considere suffit a etablir toute PAri-thmetique actuelle des nombres ordinaux. Ce modę de proceder semble etre d'ailleurs le seul admissible, etant donnę que la dis-cipline en question n'a pas ete jusqu'a present axiomatisee d'une faęon convenable.

Enfin, M. Tarski a examine ce systeme d'axiomes (que nous appellerons pour abreger „systeme U”) au point de vue d'exigences de la Methodologie des Sciences deductives. Voici les resultats les plus importants de cette etude:

1 (T)• Les axiomes du systeme U sont compatibles, si seulement il en est de meme des axiomes du systeme de la Theorie des Ensembles de M. Z e r m e 1 o sans l'axiome du c/joix, mais augmente de faxiome de substitution de M. Fraenkel¹).

*) Cf. notę *^ł) de la page 310.