1442680460

Projekt NUMPRESS, Zad. 2: Program NUMPRESS-Explicit: podstawy teoretyczne

gdzie e G^w oraz

x<²> £ r<²> :    ||x<¹>-x<²>|| = min ||x« - x<²>||,    (43)

x<²>er<²>

gdzie ć/⁽¹⁾ jest skończonym zbiorem punktów dyskretyzujących powierzchnię T⁽¹⁾, a x⁽²⁾ jest najbliższym punktem na aproksymacji powierzchni r*²'.

W sformułowaniu dyskretnym zagadnienia kontaktowego warunki (14) są zapisane dla każdego węzła ze zbioru G^ w następującej postaci:

g(xW) > 0,    F_n(x<¹⁾) < 0,    F_n(x^¹⁾)p(x<¹⁾) = 0,    (44)

gdzie F_n(xi¹⁾) jest składową normalną całkowitej siły kontaktu F_c*¹ ’ działającej na węzeł X.!¹¹

F_c⁽¹⁾ = F_n + F_s = F„n⁽²⁾ + F_s,    (45)

F_s - składowa styczna siły kontaktu, n*²* - jednostkowy wektor normalny do aproksymowanej powierzchni kontaktowej Siły kontaktu zastępują powierzchniowe oddziaływanie kontaktowe w pewnym otoczeniu węzła.

Spełnienie warunku (44)i w ogólnym przypadku nie wyklucza penetracji węzłów dyskretyzujących powierzchnię T*²* przez aproksymację powierzchni W sformułowaniu dyskretnym warunek braku penetracji należy sprawdzić obustronnie, albo dopuścić pewną penetrację węzłów jednej z powierzchni.

W sformułowaniu dyskretnym zagadnienia kontaktowego warunki przylegania/poślizgu (16)—(18) są również określone dla węzłów:

(46)

v₈

0< 0,

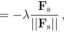
A > 0,    <ł> A = 0.

(47)

(48)

Całkowita praca przygotowana oddziaływania kontaktowego 8W_C w sformułowaniu dyskretnym może być określona jako suma prac przygotowanych (5w_c)i sił kontaktu w poszczególnych węzłach

n_c

iW_c = £(Sw_c),    (49)

gdzie n_c jest liczbą węzłów znajdujących się w kontakcie w danej chwili.

Praca przygotowana sił kontaktu w jednym węźle Sw_c może być wyznaczona z zależności analogicznej do równania (29)

Sw_c = — Fj¹) • (<5u⁽¹⁾ - <5u^),    (50)

- przemieszczenia przygotowane badanego węzła, a <5u⁽²⁾ - przemieszczenia przygotowane rzutu badanego węzła na aproksymowaną powierzchnię drugiego ciała.

Biorąc równanie (41) przemieszczenie przygotowane punktu można zapisać w następującej postaci:

<Ju⁽²⁾ = ]TiV_i(x⁽²⁾)<Suf⁾    (51)

12