1442680461

Projekt NUMPRESS, Zad. 2: Program NUMPRESS-Explicit: podstawy teoretyczne

Wstawiając (51) do (50) otrzymuje się

Swc = F_c⁽¹> ■ ^-6u⁽¹⁾ + ^ JVi(x⁽²⁾)5u<²⁾ j    (52)

co można przedstawić jako

Sw_c = 5u_c^Tf_c,    (53)

gdzie

u_c = {u<‘> uf) ... ug,}^T    (54)

f_c = {-F₀⁽¹⁾ jV,(X<²>) F_c<'> ... JV" (x<²>)F_c<¹>}^t .    (55)

Wstawiając zależności dyskretyzacyjne do równania (28), zasadę prac przygotowanych dla dyskretyzowanego zagadnienia kontaktowego można zapisać w następującej postaci, porównaj równanie (57):

(ćr_e)^T (J pN^TNdS)_ej r„ + (ór₆)^T ^J B^Tffdfi,

- (5r_s)^T (J N^Tpbdn_ej - (5r_c)^T (J N^Tt dr_t^ - ^ću/f_c = 0. (56)

Równanie (56) można zapisać w następującej postaci

(ór)^T (Mf + F^int - F^ext - F^cont) = 0.    (57)

gdzie wprowadzono definicje globalnej macierzy mas M, globalnych wektorów uogólnionych parametrów (przemieszczeń) węzłowych r oraz węzłowych sił wewnętrznych, zewnętrznych i kontaktowych, F^int, F^ext i F^cont, które otrzymuje się poprzez złożenie macierzy mas m_e oraz odpowiednich elementowych wektorów r_e, f_e^int, f_e^ext i f_c:

^nel    Cnel    ®nel    n_nc    ^nel

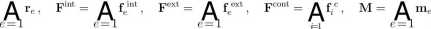
(58)

gdzie A jest standardowym operatorem agregacji globalnych wektorów i macierzy (zob. [13]), a elementowy wektor sił wewnętrznych f_e^mt, elementowy wektor sił zewnętrznych f_e^ext oraz elementowa macierz mas m_(i są dane następującymi wzorami:

f“ = [ B^T<rdn_e,    (59)

JSie

f “‘= f N^Tpbdn_e+ [ N^Tt dr_e,    (60)

Jn_e    Jr_enr_a

m_e = [ pN^TNdf2_e.    (61)

JUe

Równanie skalarne (57) musi być spełnione dla dowolnych wariacji przemieszczeń węzłowych Sr, skąd wynika, że musi być spełniony następujący układ równań

Mf + F^int - F^ext - F^cont = 0,    (62)

13