1442680475

Projekt NUMPRESS, Zad. 2: Program NUMPRESS-Explicit: podstawy teoretyczne

i znika poza obszarem kontaktu

i„ = 0 dla x⁽¹⁾ 6 r™¹ - r‘.    (13)

Ograniczenia dla funkcji odstępu między ciałami i oddziaływania w kierunku normalnym można zebrać w następującej postaci [18, 34]:

g> 0, t_n < 0, t_ng = 0.    (14)

Warunki (14) są znane jako warunki Kuhna-Tuckera dla kontaktu w kierunku normalnym.

Oddziaływanie kontaktowe w kierunku stycznym t_s, powodowane tarciem, przeciwdziała poślizgowi charakteryzowanemu przez względną prędkość w punkcie styku v_s. Przyjmując g = 0 i g — 0 prędkość poślizgu w punkcie pokrywającym się z punktem jest dana równaniem

v, = v<²)(x<²))-v(¹>(xl¹>).    (15)

Zagadnienie tarcia można sformułować analogicznie do zagadnienia plastyczności z niesto-warzyszonym prawem płynięcia [20]. Przy założonym modelu tarcia Coulomba zagadnienie tarcia można opisać przez następujący układ równań [19, 18, 29, 34]:

• funkcja poślizgu

<t>= INI -/i|«n|,

(16)

gdzie /i oznacza współczynnik tarcia Coulomba,

• prawo poślizgu

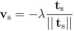
(17)

• warunki Kuhna-Tuckera określające warunki poślizgu, przylegania i wzajemnego wykluczania się przylegania i poślizgu

0<O, A > 0,    </>A = 0.    (18)

Sformułowanie lokalne zagadnienia brzegowo-początkowego dla układu dwóch kontaktujących się ciał odkształcalnych B^^a\ a= 1,2, dane jest przez następujący układ równań:

•    zasada zachowania masy

p(^a>(X^w,t)J(xW.t) =p<“>(X^<a>), X^w e t!^w°, f e [0, T],    (19)

•    równania ruchu (równania Cauchy’ego)

V ' <7⁽“> +    b<“> = p<“> a<“>,    x<“> e n<“>‘, t € [0, T],    (20)

•    naprężeniowe warunki brzegowe

n^w . ir^(a) = t^(o), x<“> e ri“>*, t e [0, T],    (21)

•    przemieszczeniowe warunki brzegowe

u^(a) = u^(a), x^(a) 6 ri^a)ł, t € [0, T\,    (22)

8