357502989

5

1.1. GRUPY, PODGRUPY, HOMOMORFIZMY

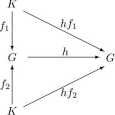
Rozważymy teraz własność homomorfizmów dualną w stosunku do kategoryjnej monomorficz-ności. Dualność ta polega na tym, że w definicji 1.1.1 zmieniamy kierunki działania wszystkich homomorfizmów.

Definicja 1.1.2. Homomorfizm grup h : G' —* G nazywa się epimorfizmem kategoryjnym grupy G' w grupę G jeśli dla dowolnej grupy K i homomorfizmów fi, f₂ '■ G —* K mamy następującą implikację:

fih = f₂h =>• fi = f₂.

Homomorfizmy występujące w tej definicji tworzą następujący diagram:

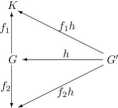
I<

Stwierdzenie 1.1.3. Jeśli homomorfizm grup h : G —* G' jest odwzorowaniem injektywnym, to h jest monomorfizmem kategoryjnym grupy G w grupę G'.

Jeśli homomorfizm grup h : G' —> G jest odwzorowaniem surjektywnym, to h jest epimorfizmem kategoryjnym grupy G' w grupę G.

Dowód. W oznaczeniach definicji 1.1.1 zakładamy, że a G K oraz hfi = hf₂. Wtedy = (hfi)(a) = (hf₂)(a) = h(f₂{a)).

Jeśli h jest odwzorowaniem injektywnym, to stąd otrzymujemy fi(a) — f₂(a). Wobec tego fi — f₂. Podobnie, w oznaczeniach definicji 1.1.2 zakładamy, że a € G oraz f\h — f₂h. Jeśli h jest odwzorowaniem surjektywnym, to istnieje b € G' taki, że a — h(b). Wobec tego

/i(a) = h(h(b)) = (hh)(b) = (f₂h)(b) = f₂(h(b)) = f₂(a).

Stąd fi = f₂.    □

Injektywny homomorfizm grup h : G —* G' nazywa się zwykle monomorfizmem, zaś homomorfizm surjektywny nazywa się epimorfizmem. Tak więc każdy monomorfizm grup jest monomorfizmem kategoryjnym i każdy epimorfizm grup jest epimorfizmem kategoryjnym. Niestety, twierdzenia odwrotne nie są prawdziwe i w związku z tym istnieje konieczność rozróżniania morfizmów grupowych i kategoryjnych. Odpowiednie kontrprzykłady podajemy w rozdziale 5.

Homomorfizm, który jest równocześnie monomorfizmem i epimorfizmem nazywa się izomorfizmem.

Najważniejszym przykładem homomorfizmu grup jest homomorfizm kanoniczny k : G —* G/H, gdzie H jest dowolną podgrupą normalną grupy G. Jest on określony następująco: n(a) = aH dla a € G. Jest to epimorfizm oraz ker k = H. A więc każda podgrupa normalna H grupy G jest