357502990

6

ROZDZIAŁ 1. GRUPY

jądrem pewnego homomorfizmu grupy G w odpowiednio dobraną grupę G' (na przykład na grupę ilorazową G/H).

Sformułujemy teraz trzy podstawowe twierdzenia o homomorfizmach grup.

Twierdzenie 1.1.4. (Twierdzenie o faktoryzacji.)

Jeśli h : G —* G' jest homomorfizmem grup, J := ker h oraz k : G —* G/J jest homomorfizmem kanonicznym, to istnieje dokładnie jeden monomorfizm h* : G/J —► G' taki, że h — h* o k, a więc taki, że następujący diagram jest przemienny:

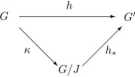
Homomorfizm /i* definiuje się kładąc h»(aJ) = h(a) dla a € G.

Z tego twierdzenia wynika, że każdy homomorfizm h : G —* G' ma rozkład postaci

a -*-> a/j i. im/i -U a',

gdzie k jest homomorfizmem kanonicznym, h* jest monomorfizmem oraz j jest włożeniem. Innym bardzo użytecznym faktem jest następujący wniosek.

Wniosek 1.1.5. Jeśli h : G —* G' jest epimorfizmem grup, to homomorfizm h* jest izomorfizmem i wobec tego

G/kerh = G'.

Dla grupy G symbolami SubG i NSubG oznaczamy odpowiednio zbiór wszystkich podgrup grupy G i zbiór wszystkich podgrup normalnych grupy G. Jeśli H jest podgrupą grupy G, to Sub// G i NSub//G oznaczają odpowiednio zbiór wszystkich podgrup grupy G zawierających podgrupę H i zbiór wszystkich podgrup normalnych grupy G zawierających podgrupę H.

TWIERDZENIE 1.1.6. (Twierdzenie o odpowiedniości.)

Niech h : G —* G' będzie epimorfizmem grup. Wtedy przyporządkowanie

h* : SubjG —► SubG',    h*{H) = h{H)

każdej podgrupie H grupy G zawierającej jądro J = ker h jej obrazu h{H) w grupie G' jest bijekcją taką, że /i*(NSub;G) = NSubG'.

Ponadto, dla każdej podgrupy normalnej H grupy G zawierającej jądro J = ker h mamy izomorfizm G/H £2 G'/h(H).

Dowód. Dla L € SubG' mamy h(h~^l(L)) — L, zatem h* jest odwzorowaniem surjektywnym. Dla dowodu, że h* jest odwzorowaniem injektywnym przypuśćmy, że J < Hi, H2 < G oraz h{H\) = h(H2). Wtedy na podstawie (1.3) mamy

i?i = h~^l(h(Hi)) = h-'(h(H₂)) = H₂.

A więc h* jest bijekcją.

Niech teraz J < H < G (to znaczy H € NSubjG). Wtedy dla x € G' oraz a € G takiego, że h(a) = x mamy

x ■ h(H) ■ X-¹ = h(a) ■ h(H) ■ h(a= h(aHar^l) = h(H).

Stąd wynika, że h(H) € NSubG'. Zatem zacieśnienie h* do NSub./ G jest injekcją w zbiór NSubG'. Pozostaje pokazać, że zacieśnienie to jest surjekcją. Niech więc L € NSubG'. Dla każdego a € G mamy

h(a ■ h~^l(L) ■ a^-1) = h(a) ■ L • h(a)^-1 = L.