6700449609

Zadanie 5.57. Niech f: IR -» IR będzie dana następująco:

o,

[0,1),

C —x², dla x < f(x) = i x, dla x 6

(2x-1, dla x > 1.

Zbadać, czy f jest bijekcją, a jeśli tak, to wyznaczyć f ¹.

Zadanie 5.58. Pokazać, że funkcja f(x) = x + £, x ^ 0, jest funkcją nieparzystą, ściśle rosnącą przedziale [1,oo) oraz ściśle malejącą na przedziale (0,1).

Zadanie 5.59. Niech g: IR —^ IR będzie określona następująco:

	dla x <
3,	dla x =
x^2 +2x+ 1,	dla x >

(a)    Sprawdzić, czy g jest różnowartościowa,

(b)    wyznaczyć g(IR),

(c)    wyznaczyć g ¹.

Zadanie 5.60. Niech f: IR -> IR będzie określoną wzorem f(x) = ||x — 11 — 2|. Wyznaczyć zbiór

f~'«-oo,2)).

Zadanie 5.61. Sprawdzić, czy funkcja f: IR —^ IR określona wzorem f(x) = , * j, jest różnowartościowa. Wyznaczyć f(IR).

sie dana następująco:

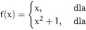
Zadanie 5.62. Niech f: IR —> IR

0,

0.

Wyznaczyć zbiór f ¹ (A), gdzie A = [—1,1) U (2).

Zadanie 5.63. Niech g: IR —> IR będzie określona następująco:

,, fx + §, dlax«j,

⁹ * ~ |-2x + 2, dla x > |.

Wyznaczyć zbiory g(A),g~^] (B), gdzie A = (0,5],B = (0,1) U{2}.

Zadanie 5.64. Pokazać, że funkcja f: IR -»IR określona wzorem f(x) = jest ściśle rosnąca Wyznaczyć f(IR) oraz skonstruować funkcję odworotną do f.

Zadanie 5.65. Pokazać, że funkcja f(x) = In ^x + </1 + x²j jest nieparzysta.

Zadanie 5.66. (*) Niech f: D —> IR, gdzie D C IR oraz g: f(IR) —> IR. Pokazać, że

(a)    jeśli funkcję f i g są jednocześnie rosnące lub jednocześnie malejące, to g o f jest rosnąca,

(b)    jeśli f jest rosnąca, a g malejąca, to g o f jest malejąca,

(c)    jeśli f jest malejąca, a g rosnąca, to g o f jest malejąca.