7223156831

71

*

A Paide de la fonction Discrete Fourrier Transform (fft) de Matlab, le contenu harmoniąue des signaux modulćs a ete extrait pour chacun des convertisseurs. Les rćsultats ont ćtć obtenus pour une pćriode d’ćchantillonnage de lps, une frćąuence de commutation de 10kHz et une frćąuence du signal intelligent de 100Hz. L’analyse s’est limitće & P amplitudę de rharmoniąue de commutation (SwHarm) ś 10kHz puisqu’ćtant la plus ćlevće. Le spectre des signaux modulćs varie selon 1’amplitude du signal intelligent, c’est pourąuoi la Figurę 3.16 exprime 1’amplitude de SwHarm selon le ratio de 1’amplitude crete du signal intelligent sur la tension maximale de sortie du convertisseur; pour le convertisseur a deux niveaux, il s’agirait de 1’indice de modulation.

Ampttuóe do rharmooique de cornmutition scłon fimpltude du sinus moduł*

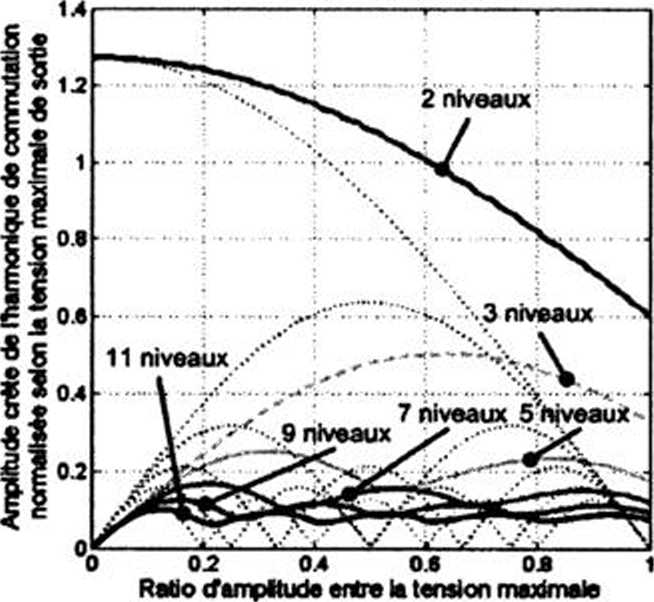
de sortie et łe tension crtte du sinus modiM

Ampitude de Phamxxnquo de coovnu(«tion selon rempitude du tmpćze modii6

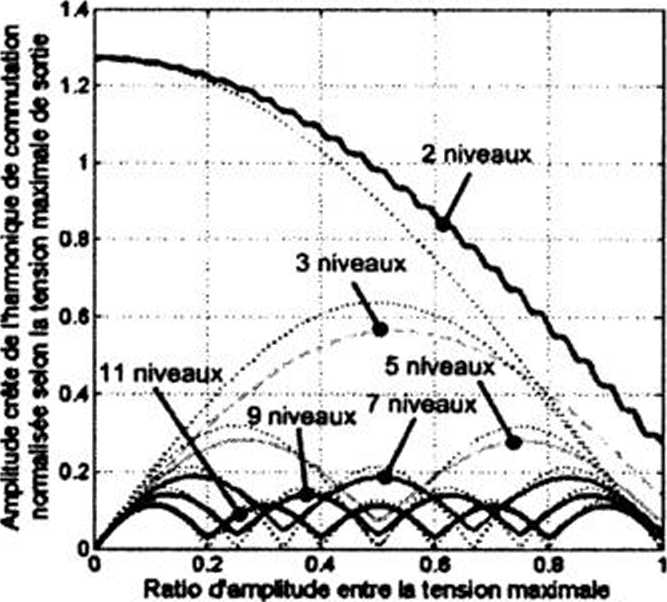
de sortie et ii tension crtte du trsoóze modLM

Figurę 3.16 Amplitudę crete normalisće de rharmoniąue de commutation

pour des convertisseurs de S niveaux.

Sur les deux graphiąues de la Figurę 3.16, des lignes pointillćes ont ćte ajoutees pour indiąuer 1’amplitude de SwHarm lorsąue le signal est continu. On obtient analytiąuement 1’ amplitudę crete de cette harmoniąue pour un signal continu en calculant les coefficients de Fourrier. L’ćąuation 3.6 dćcrit cette relation et la Figurę 3.17 identifie les variables de cette relation. Ajoutons seulement que k est 1’ordre de rharmoniąue de commutation. Pour k = 1, le coefficient obtenu est celui de la fondamentale & la frćąuence de commutation (Fs). En comparant les deux graphiąues de la Figurę 3.16, on s’aperęoit ąue le spectre de 1’onde