7292100728

Tyczenie prostych boz przeszkód. 439

0 ile nie znamy AC' i C'B, przesuwamy się po zmierzeniu na punkcie C* kąta yj o pewien odstęp (<2) do punktu C", w którym mierzymy kąt *(₂. Przesuniecie w kierunku poprzecznym d», konieczne, aby znaleźć się w punkcie C, leżącym na prostej A—B, wynosi:

Kąty należy mierzyć bardzo starannie w

obu położeniach lunety.    —______

Przesunięcie poprzeczne uskuteczniamy zawsze w kierunku kata A C 'B mniejszego 7

od 180°.    ^H    ----

3. Długość prostej wynosi około    *'<8- ¹⁰⁶-

iO km. Tu nie wystarczają zwykle sposoby podane poprzednio, lecz nalęźy oprzeć się na trian-gulncji państwowej lub założyć sieć specjalną, redukującą sie zazwyczaj do łańcucha trójkątów (por. fig. 105).

Po wyrównaniu sieci, obliczamy spółrzedne jej punktów w dowolnie przyjętym układzie, np. x_A = 0, y_A — 0, (o)_AJ} — O°, a następnie 1

tang a

i = (a)_{0 c} — (a)_n

(°)fb — (^a)jy ai

przyczem tang (a)_D

Vc~ ‘Jd

(°)e . C ~~ (^a).l. 1»

~VD

- x

n

O)f b ■■

■VC'

tang (a)_{E G} = -

Spółrzędne punktu G otrzymamy z równań:

Vf~Vb _{    .    . Vd

V — Vb'- “-- \^x~xj_f) 1 y =

x

F

x

B

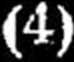
odpowiadających prostym BF i AD, zatem

VF ~ Vb

^XB ~ Vb

y f vb vd

^xn' ^tftn£> (^a)y/. f • Vb

taug («)/*. j!.-~tang(rt)_yL D

^ld

^XB — Vn cotang {g)_H F 1 — tang (a) _t f) cotang

'Jg — ^xa

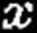
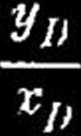
Xj_{ . tang (d)_{E F}-y_n tang {ct)ji _Fcotang (a)₄ D-

VF~ Vb

x_F—x_u

Vf— 'Jb ^x

101