Odchylenie standardowe - klasyczna miara zmienności, obok
średniej arytmetycznej najczęściej stosowane pojęcie statystyczne.
Odchyleniem standardowym nazywamy dodatni pierwiastek z
wariancji.
Powtarzając wielokrotnie pomiar tej samej wielkości, zauważamy
rozrzut wyników wokół pewnej wartości, którą uznajemy za
prawdziwą. Zwykle najlepszym przybliżeniem wartości prawdziwej
jest wartość średnia uzyskanych wyników.

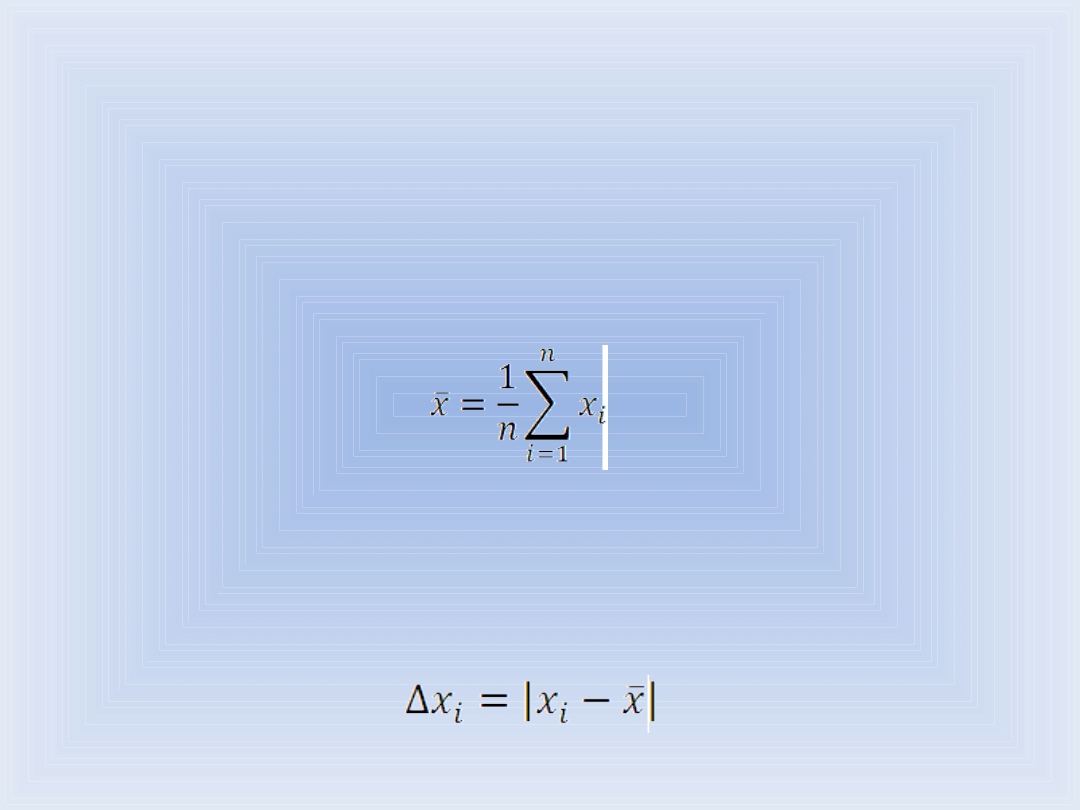
Niepewność pojedynczego pomiaru to wartość bezwzględna
różnicy pomiędzy pomiarem x

i

,a wartością prawdziwą X , której

nie znamy. W praktyce obliczamy ją jako odchyłkę ∆ x

i

, czyli

wartość bezwzględną różnicy pomiędzy danym pomiarem, a wartością
średnią.

Odchyłkę tę utożsamiamy z błędem bezwzględnym i-tego pomiaru.
Dla n pomiarów otrzymujemy n takich odchyłek. Wygodniejsze
byłoby określenie jednej odchyłki uniwersalnej dla wszystkich n
pomiarów. W tym celu najczęściej wyznaczamy dla danej serii
wyników tzw. odchylenie standardowe S pojedynczego pomiaru.
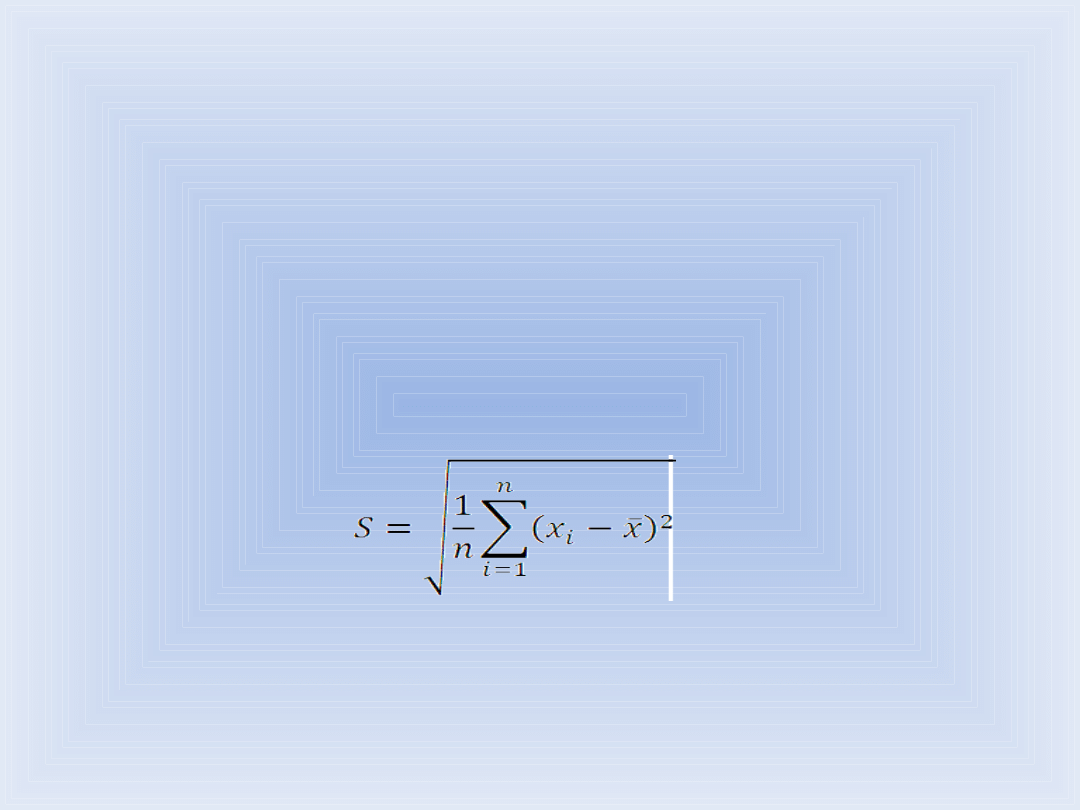
Odchylenie standardowe S obliczmy jako pierwiastek z sumy
kwadratów odchyłek podzielonej przez liczbę pomiarów n.

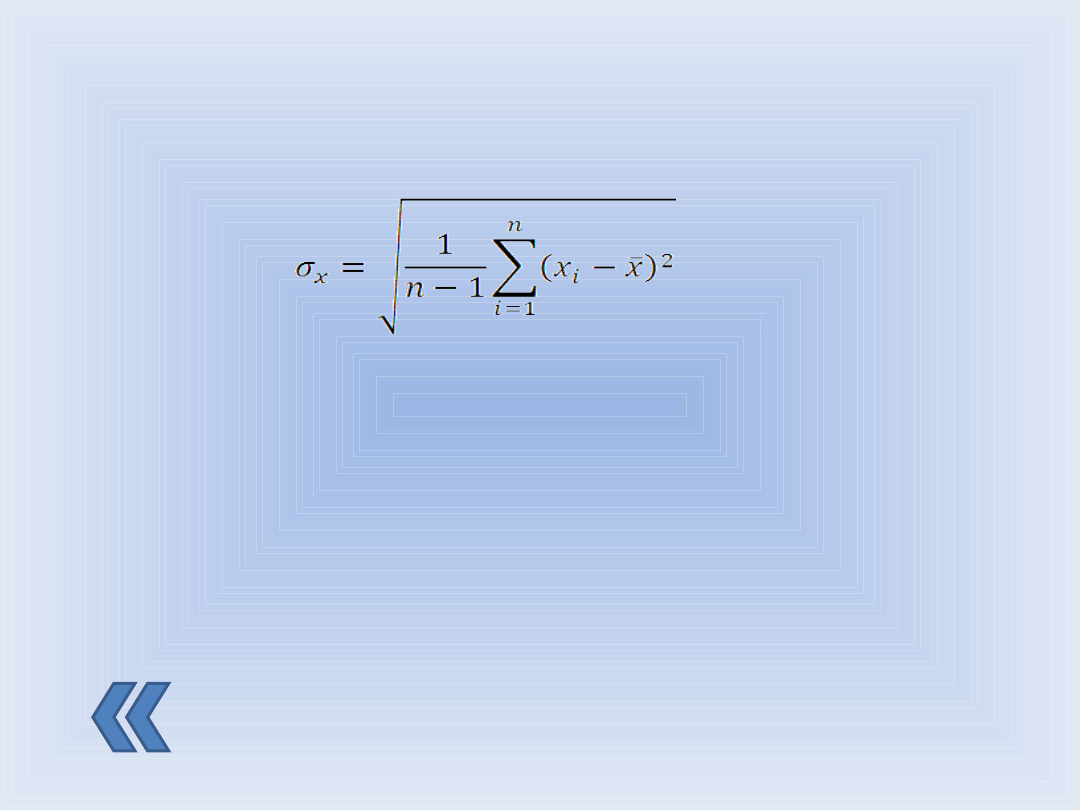
Istnieje także inna definicja odchylenia standardowego. Pewne
argumenty teoretyczne przemawiają za zamianą czynnika n w
mianowniku wyrażenia S na n-1 i za zdefiniowaniem odchylenia
standardowego pomiarów oznaczonego teraz jako σ

x

- wzorem :

Modyfikacja powoduje, nieznaczne zwiększenie wartości σ

x

względem S. Koryguje to tendencję niedoceniania niepewności
pomiarów, szczególnie dla małej ilości pomiarów n . Różnica
pomiędzy odchyleniami standardowymi policzonymi za pomocą obu
definicji jest liczbowo prawie zawsze nieznacząca. Nawet jeśli
przeprowadzamy tylko 5 pomiarów N=5, różnica pomiędzy pierwszą
a drugą definicją nie jest dla większości zastosowań znacząca.
Niemniej zawsze lepiej korzystać z bardziej ostrożnej definicji σ

x

.

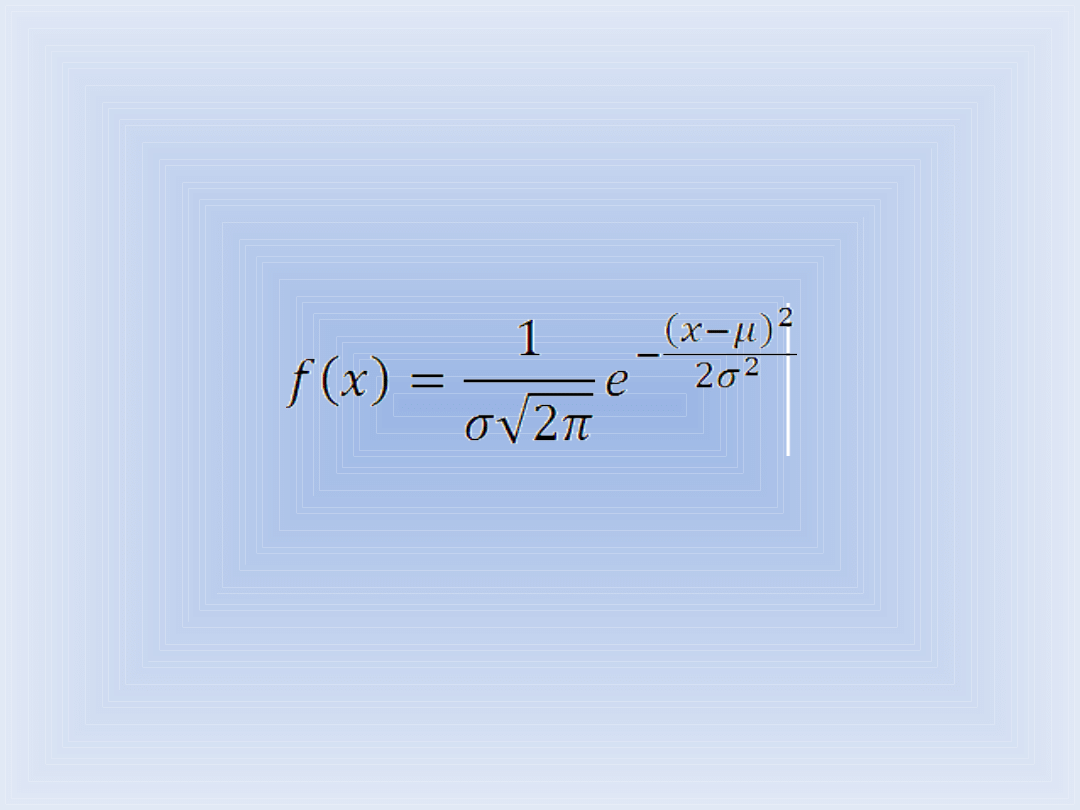
Autorstwo rozkładu normalnego przypisuje się K.F. Gaussowi, który
opisał go na podstawie analizy błędu obserwacji. Do rozkładu
normalnego prowadzi taki proces kształtowania zjawiska, w ramach
którego oddziałuje na nie duża liczba niezależnych czynników których
wpływ traktowany odrębnie, jest mało znaczący. Funkcja gęstości
prawdopodobieństwa f(x) rozkładu normalnego wyraża się wzorem:

gdzie: μ- wartość oczekiwana,

σ- odchylenie standardowe,
x- pojedynczy pomiar.

Rozkład normalny jest zatem w pełni scharakteryzowany przez dwa
parametry wartość oczekiwaną i odchylenie standardowe.

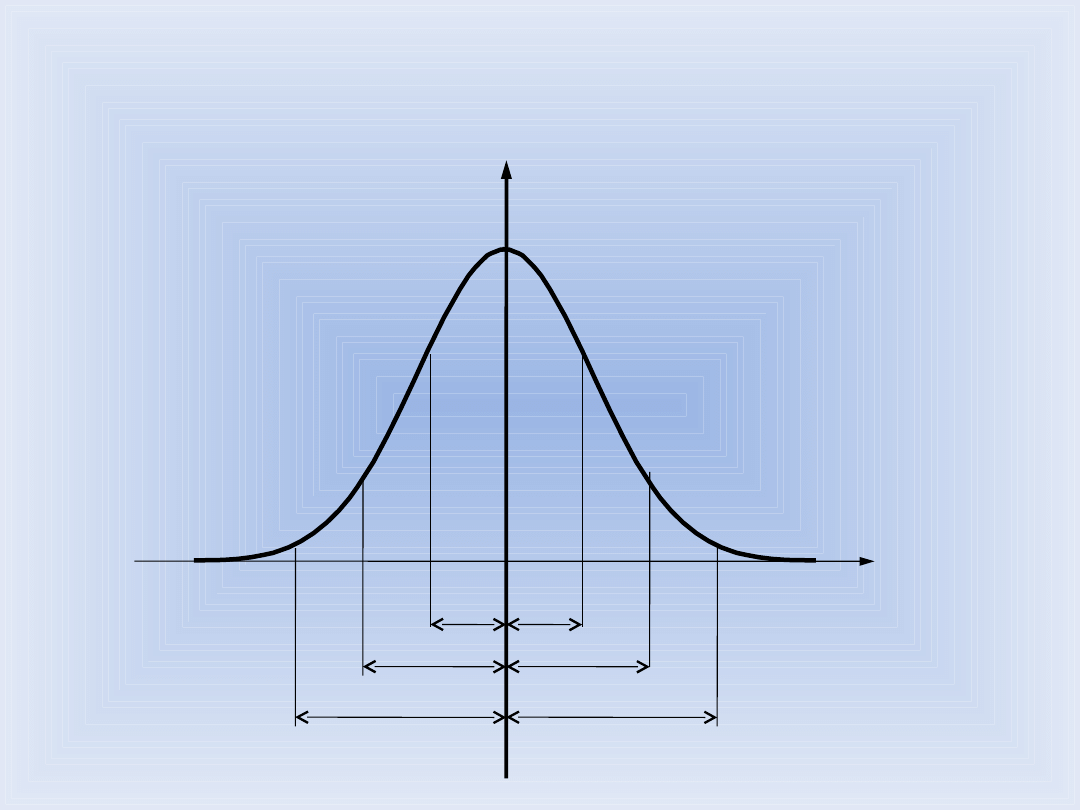
Kształt krzywej gęstości prawdopodobieństwa dla rozkładu normalnego
przedstawiono poniżej.





2



2



3



3



μ

x

Podstawowe właściwości rozkładu normalnego:

• jest symetryczny względem wartości oczekiwanej,

• gęstość prawdopodobieństwa jest największa w najbliższym
otoczeniu wartości oczekiwanej,

• prawdopodobieństwo wystąpienia zmiennej losowej w
charakterystycznych przedziałach w otoczeniu wartości oczekiwanej
wynoszą

- P(μ-σ ≤ x ≤ μ+σ) = 0,6826 (68,26%),
- P(μ-2σ ≤ x ≤ μ+2σ) = 0,9544 (95,44%),
- P(μ-3σ ≤ x ≤ μ+3σ) = 0,9973 (99,73%),

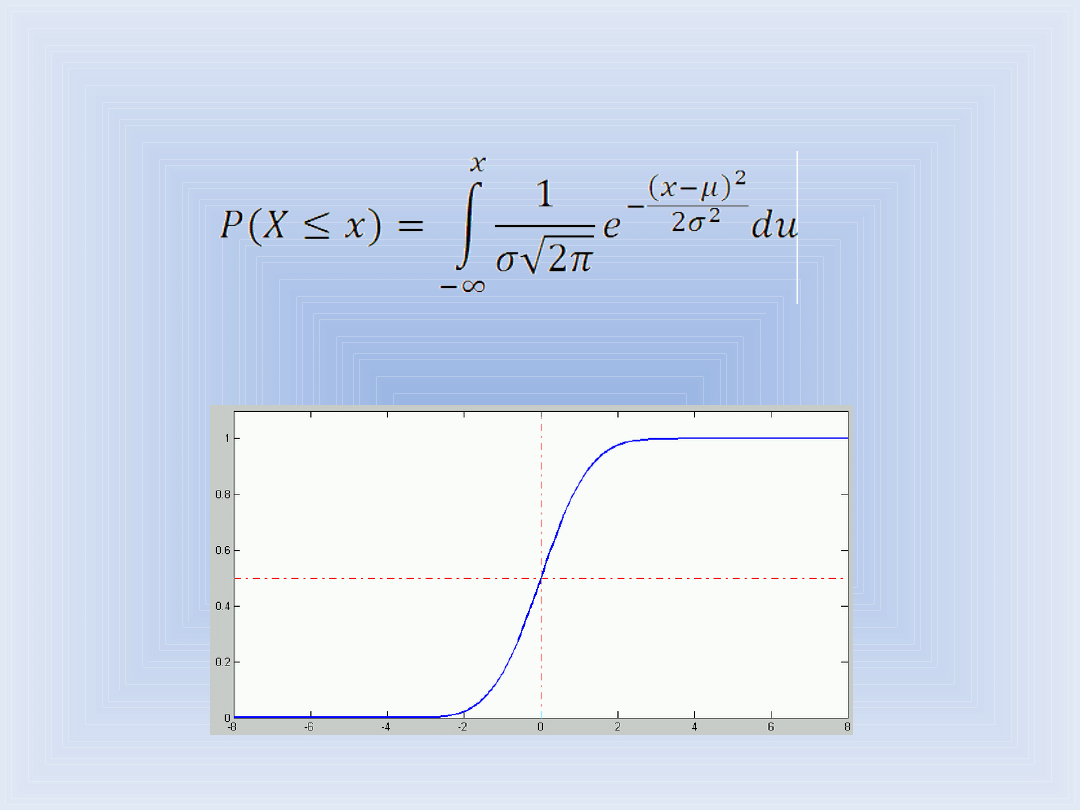
Dystrybuanta - kumulacyjna funkcja rozkładu- jest definiowana jako
prawdopodobieństwo tego, że zmienna X ma wartości mniejsze bądź
równe x i w kategoriach funkcji gęstości wyrażana jest (dla rozkładu
normalnego) wzorem:

Całki powyższej nie da się policzyć dokładnie metodą analityczną. W
konkretnych zagadnieniach do obliczenia wartości dystrybuanty
stosuje się zatem tablice statystyczne (bądź też odpowiednie
kalkulatory czy oprogramowanie komputerów).

D

y

st

ry

b

u

a

n

t

a

Zmienna
losowa

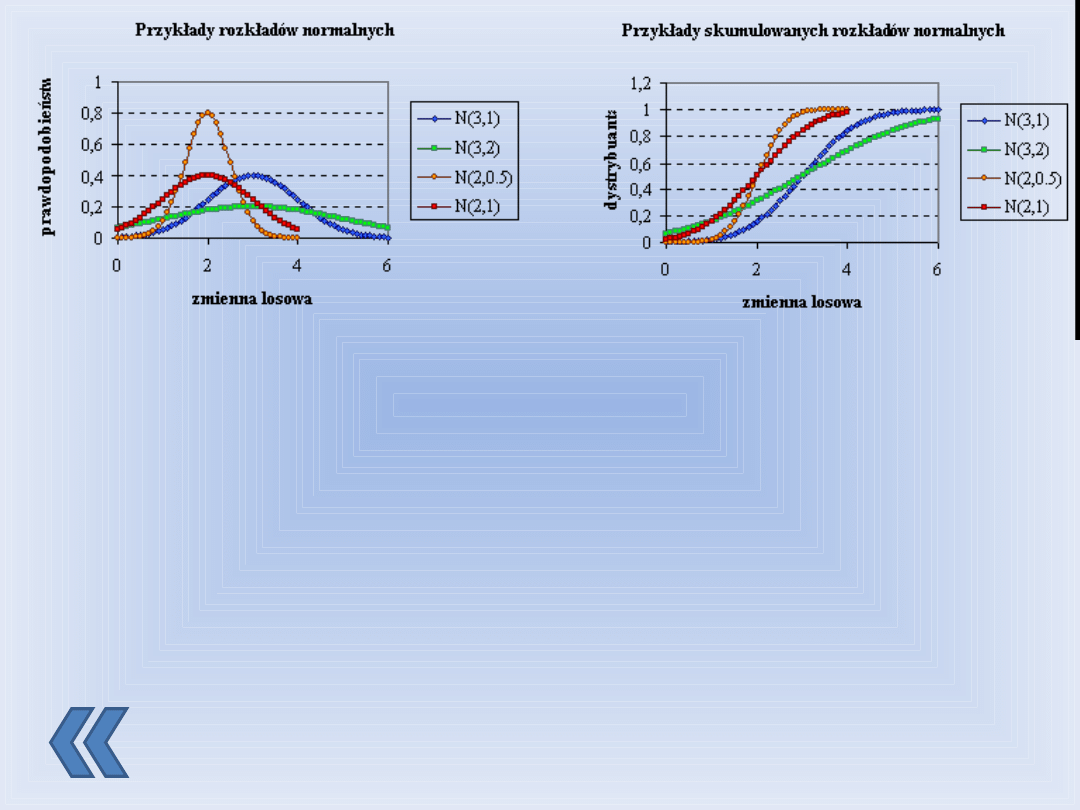
Dystrybuanta zmiennej losowej jest całką z funkcji rozkładu
normalnego Gaussa. Punkt przegięcia wykresu dystrybuanty
odpowiada maksymalnej wartości wykresu rozkładu Gaussa.
Znając wartości dystrybuanty można obliczyć prawdopodobieństwo
wystąpienia w dowolnym przedziale [x

1

,x

2

] z zależności:

P(x

1

≤ X ≤x

2

)=F(x

2

)-F(x

1

)

Błędy pomiarów można rozważać jako zmienne losowe ciągłe o
rozkładzie normalnym, dlatego sposób wyznaczania
prawdopodobieństwa występowania zmiennej w określonym przedziale
z powyższego wzoru może być użyteczne przy analizie wyników badań.