Zmodyfikowany algorytm simpleks

Rozważamy liniowy model decyzyjny o n zmiennych decyzyjnych i m ograniczeniach

(1)

(2)

(3)

rozszerzony o n ograniczeń "widełkowych"

(4)
(j=1,2, ... ,n)

Problem (1-4) nazywamy zadaniem ograniczonym (z ograniczeniami z góry).

Problem (1-3) nazywamy zadaniem wolnym. Rozwiązanie bazowe zadania wolnego:

(5)

Zbiór zmiennych zadania wolnego (1-3) dzielimy na trzy podzbiory, tj.

1. zbiór B - zbiór zmiennych bazowych

2. zbiór Z - zbiór zmiennych niebazowych przyjmujących dla bazy B wartości zerowe

3. zbiór G - zbiór zmiennych niebazowych przyjmujących dla bazy B wartości górne

Oznaczmy przez
rozwiązanie bazowe
zadania wolnego (1-3) skorygowane zachowaniem się zmiennych niebazowych tego zadania. Będą to wartości zmiennych bazowych zadania ograniczonego (1-4) .

(6)
(i=1,2, ... ,m)

gdzie:
są elementami tablicy simpleksowej
generowanej przez bazę B zadania wolnego (1-3).

Wartość funkcji celu
zadania ograniczonego (1-4) wynosi

(7)
(i=1,2, ... ,m)

gdzie:
są wskaźnikami optymalności w bazie B zadania wolnego (1-3).

Kryterium optymalności

Baza B zadania wolnego (1-3) generuje rozwiązanie optymalne zadania rozszerzonego (1-4), gdy dla zmiennych niebazowych spełnione są żądania (8) i (9).

(8)
dla każdego

(9)
dla każdego

Kryterium wejścia

Zmienną wchodzącą
powinna być wybrana spośród tych zmiennych niebazowych
lub zmiennych niebazowych
, której wskaźnik optymalności "najmocniej popsuł" kryterium optymalności (8) lub (9).

(10)

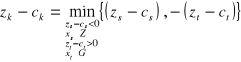
Kryterium wyjścia

Kryterium wyjścia realizowane jest jedną z dwóch ścieżek w zależności od statusu zmiennej wchodzącej
wytypowanej przez kryterium wejścia (10), tj.

I. zmienna wchodząca
ma status Z (
) lub

II. zmienna wchodząca
ma status G (
).

W ramach każdej ze ścieżek rozważane są trzy warianty postępowania:

1. zmienna opuszczająca bazę przejdzie do zbioru Z; zmiana bazy B zadania wolnego,

2. zmienna opuszczająca bazę przejdzie do zbioru G ; zmiana bazy B zadania wolnego lub

3. zmienna wchodząca
nadal pozostanie niebazową zmieniając tylko swój status na przeciwny (z Z na G - w ścieżce I lub z G na Z - w ścieżce II); baza B zadania wolnego (1-3) nie ulegnie zmianie.

Ścieżka I (zmienna wchodząca ma status Z;
tj.
)

Warianty postępowania:

1. Zmienna opuszczająca bazę otrzyma status Z. Alternatywny przyrost wartości
zmiennej wchodzącej
wynika z analizy ilorazów wyjścia i wynosi

(11)

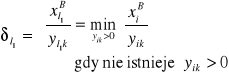
2. Zmienna opuszczająca bazę otrzyma status G. Alternatywny przyrost wartości
zmiennej wchodzącej
wynika z analizy ilorazów wyjścia i wynosi

(12)

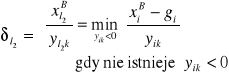
3. Zmiana statusu zmiennej wchodzacej. Alternatywny przyrost wartości
zmiennej wchodzącej
odpowiadać będzie wartości górnej

(13)

O wyborze wariantu poprawy rozwiązania (wariant 1, 2 lub 3) w ramach ścieżki I roztrzygamy wybierając minimalny z alternatywnych przyrostów
zmiennej wchodzącej
, który wyznacza przyszłą wartość
tej zmiennej.

(14)

Ścieżka II (zmienna wchodząca ma status G;
tj.
)

Warianty postępowania:

1. Zmienna opuszczająca bazę otrzyma status Z. Alternatywny spadek wartości
zmiennej wchodzącej
wynika z analizy ilorazów wyjścia i wynosi

(15)

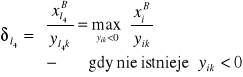
2. Zmienna opuszczająca bazę otrzyma status G. Alternatywny spadek wartości
zmiennej wchodzącej
wynika z analizy ilorazów wyjścia i wynosi

(16)

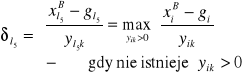
3. Zmiana statusu zmiennej wchodzacej. Alternatywny spadek wartości
zmiennej wchodzącej
odpowiadać będzie wartości górnej

(17)

O wyborze wariantu poprawy rozwiązania (wariant 1, 2 lub 3) w ramach ścieżki II roztrzygamy wybierając maksymalny z alternatywnych spadków
zmiennej wchodzącej
, który wyznacza przyszłą wartość
tej zmiennej.

(18)

Przykład

Zmodyfikowane postępowanie simpleksowe wykorzystamy do rozwiązania poniższego modelu decyzyjnego.

(1)

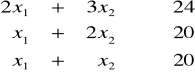
(2)

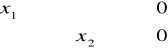
(3)

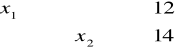
(4)

Tabele simpleksowe dla przykładu

¦

lista

zadanie

zadanie

2

4

0

0

0

−100

−100

kryterium wyjścia

zmien-nych

ogr.

wolne

ścieżka I

ścieżka II

bazo-wych

iteracja 1

24

2

3

−1

0

0

1

0

20

1

2

0

−1

0

0

1

20

1

1

0

0

1

0

0

status zmiennej

Z

Z

Z

Z

B

B

B

iteracja 2

x

x

x

x

status zmiennej

x

iteracja 3

x

x

x

x

x

x

x

x

status zmiennej

x

x

iteracja 4

x

x

x

x

x

x

x

x

status zmiennej

x

x

iteracja 5

x

x

x

x

x

x

x

x

status zmiennej

x

x

1

Zmodyfikowany algorytm simpleks M.Miszczyński KBO UŁ

---