Mariusz SZTABIŃSKI

A.O.R. sem.VIII

Ćw.

Projektowanie cyfrowego dolnoprzepustowego filtru IIR typu: Czebyszewa I, Czebyszewa II i eliptycznego.

1. Wymagania dla filtru cyfrowego:

_p= 0.02

_s= 0.001

_p= 0.4
= 1.2566

_s= 0.7
= 2.199

2. Obliczenia przed wprowadzeniem danych:

=

= 1

= 91.188
_s = 1.7501

3. Obliczenia komputerowe

*)

1. Czebyszew I rząd = 8
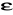
   =0.203054

2. Czebyszew II rząd = 20
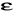
   =0.001

3. eliptyczny rząd = 6

Widać wyrażenie, że błąd dla filtru Czebyszewa II jest o wiele mniejszy w porównaniu

z Czebyszewa I, lecz wzrósł rząd filtru i to aż z 8 do 20 co powoduje problemy nume-

ryczne.

**)

Obliczenia współczynników transmitancji H(s) filtru analogowego.

H(s) =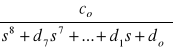

d₇ = 1.492432 c_o = 0.038472

d₆ = 3,11368

d₅ = 3,019959

d₄ = 2,9095912

d₃ = 1,7452378

d₂ = 0,8551967

d₁ = 0,2514806

d₀ = 0,0392592

***)

Transformacja transmitancji analogowej H(s) na cyfrową H(z).

H(z) = z^-S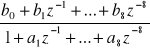

b₀ = 7,91598 10^-18 a₁= -7,966309

b₁ = 6,332079 10^-17 a₂ = 27,765683

b₂ = 2,216228 10^-16 a₃ = -55,301582

b₃ = 4,432455 10^-16 a₄ = 68,843468

b₄ = 5,540569 10^-16 a₅ = -54,850912

b₅ = 4,432455 10^-16 a₆ = 27,314983

b₆ = 2,216228 10^-16 a₇ = -7,773128

b₇ = 6,332079 10^-17 a₈ = 0,967798

b₈ = 7,915098 10^-18

Dla filtrów Czebyszewa II i eliptycznego nie musimy wypisywać współczynników

Za pomocą funkcji gafilspec stwierdzam, że założenia projektu są spełnione. Różnią

się te wyliczenia trochę od siebie co wynika z różnych metod liczenia współczynników

transmitancji H(s).

Po zmianie transformacji analogowej H(s) na cyfrową H(z) uzyskałem współczyn-

niki b_i , a_i. Charakterystyki filtru obejrzanego za pomocą funkcji gdtft dowiodły popraw-

ności zaprojektowanego filtru, więc nie było potrzeby zwiększania rzędu filtru.

---